What is transformation? In many cases a complex picture can always be treated as a combination of straight line, circles, ellipse etc., and if we are able to generate these basic figures, we can also generate combinations of them. Once we have drawn these pictures, the need arises to transform these pictures.
We are not essentially modifying the pictures, but a picture in the center of the screen needs to be shifted to the top left hand corner, say, or a picture needs to be increased to twice it’s size or a picture is to be turned through 900 . In all these cases, it is possible to view the new picture as really a new one and use algorithms to draw them, but a better method is, given their present form, try to get their new counter parts by operating on the existing data. This concept is called transformation.
The three basic transformations are
(i) Translation
(ii) rotation and
(iii) Scaling.
Translation refers to the shifting of a point to some other place, whose distance with regard to the present point is known. Rotation as the name suggests is to rotate a point about an axis. The axis can be any of the coordinates or simply any other specified line also. Scaling is the concept of increasing (or decreasing) the size of a picture. (in one or in either directions. When it is done in both directions, the increase or decrease in both directions need not be same) To change the size of the picture, we increase or decrease the distance between the end points of the picture and also change the intermediate points are per requirements.
Translation:
Consider a point P(x1 , y1 ) to be translated to another point Q(x2 , y2 ). If we know the point value (x2, y2) we can directly shift to Q by displaying the pixel (x2, y2). On the other hand, suppose we only know that we want to shift by a distance of Tx along x axis and Ty along Y axis. Then obviously the coordinates can be derived by x2 =x1 +Tx and Y2 = y1 + Ty .
Suppose we want to shift a triangle with coordinates at A(20,10), B(30,100) and C(40,70). The shifting to be done by 20 units along x axis and 10 units along y axis. Then the new triangle will be at A1 (20+20, 10+10) B1 (30+20, 10+10) C1 (40+20, 70+10) In the matrix form [x2 y2 1] = [x1 y1 1]
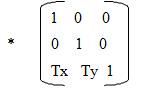
Rotation
Suppose we want to rotate a point (x1 y1) clockwise through an angle? about the origin of the coordinate system. Then mathematically we can show that
x2 = x1cos ? + y1sin? and
y2 = x1sin? – y1cos?
These equations become applicable only if the rotation is about the origin.
In the matrix for [x2 y2 1] = [x1 y1 1]
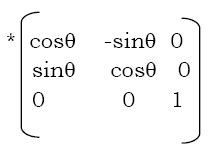
Scaling : Suppose we want the point (x1 y1) to be scaled by a factor sx and by a factor sy along y direction.
Then the new coordinates become : x2 = x1 * sx and y2 = y1 * sy
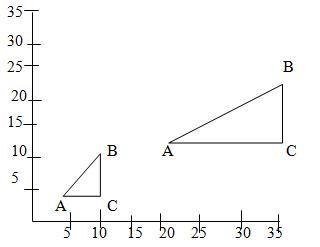
(Note that scaling a point physically means shifting a point away. It does not magnify
the point. But when a picture is scaled, each of the points are scaled differently and hence the dimensions of the picture changes.)
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular