A functional dependency is an association between two attributes of the same relational database table. One of the attributes is called the determinant and the other attribute is called the determined. For each value of the determinant there is associated one and only one value of the determined.
If A is the determinant and B is the determined then we say that A functionally determines B and graphically represent this as A → B. The symbols A → B· can also be expressed as B is functionally determined by A.
Example
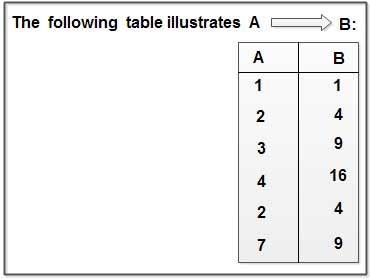
Since for each value of A there is associated one and only one value of B.
Example
Since for A = 3 there is associated more than one value of B.
Functional dependency can also be defined as follows:
An attribute in a relational model is said to be functionally dependent on another attribute in the table if it can take only one value for a given value of the attribute upon which it is functionally dependent.
Example: Consider the database having following tables:
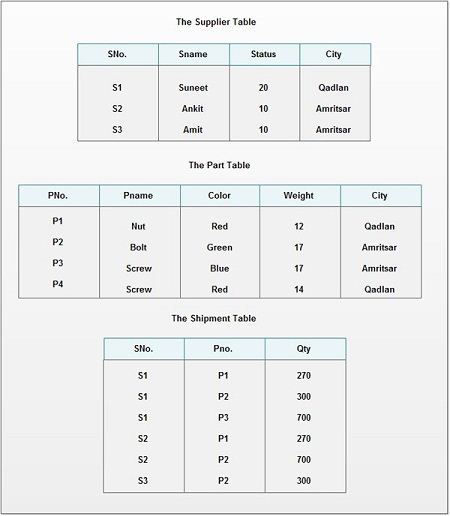
Here in Supplier table
Sno – Supplier number of supplier that is unique
Sname – Supplier name
City – City of the supplier
Status – Status of the city e.g. A grade cities may have status 10, B grad cities may have status 20 and so on.
Here, Sname is FD on Sno. Because, Sname can take only one value for the given value of Sno (e.g. S 1) or in other words there must be one Sname for supplier number S1.
FD is represented as:
Sno → Sname
FD is shown by → which means that Sname is functionally dependent on Sno.
Similarly, city and status are also FD on Sno, because for each value of Sno there will be only one city and status.
FD is represented as:
Sno – City
Sno – Status
S. Sno – S (Sname, City, Status)
Consider another database of shipment with following attributes:
Sno – Supplier number of the supplier
Pno – Part number supplied by supplier
Qty – Quantity supplied by supplier for a particular Part no
In this case Qty is FD on combination of Sno, Pno because each combination of Sno and Pno results only for one Quantity.
SP (Sno, Pno) → SP.QTY
Dependency Diagrams
A dependency diagram consists of the attribute names and all functional dependencies in a given table. The dependency diagram of Supplier table is.
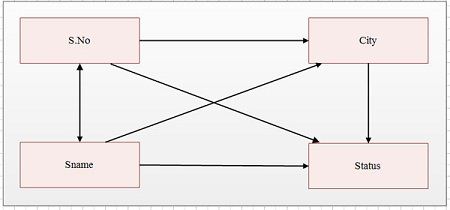
Here, following functional dependencies exist in supplier table
Sno – Sname
Sname – Sno
Sno – City
Sno – Status
Sname – City
Sname – Status
City – Status
The FD diagram of relation P is
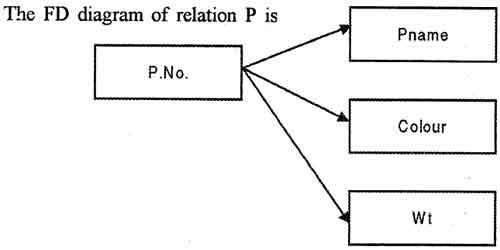
Here following functional dependencies exist in Part table:
Pno – Pname
Pno – Color
Pno – Wt
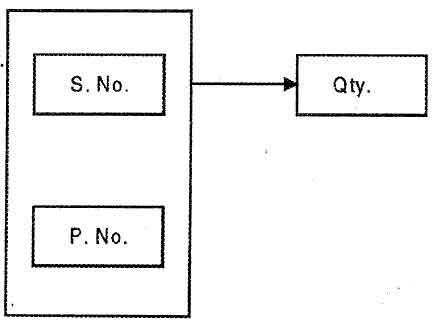The FD diagram of relation Shipment is
Here following functional dependencies exist in parts table
SP (Sno, Pno) – SP.QTY
Fully Functional Dependence (FFD)
Fully Functional Dependence (FFD) is defined, as Attribute Y is FFD on attribute” X, if it is FD on X and not FD on any proper subset of X. For example, in relation Supplier, different cities may have the same status. It may be possible that cities like Amritsar, Jalandhar may have the same status 10.
So, the City is not FD on Status.
But, the combination of Sno, Status can give only one corresponding City ,because Sno” is unique. Thus,
(Sno, Status) City
It means city is FD on composite attribute (Sno, Status) however City is not fully functional dependent on this composite attribute, which is explained below:
(Sno, Status) City
X Y
Here Y is FD on X, but X has two proper subsets Sno and Status; city is· FD .on one proper subset .of X i.e. Sno
Sno City
According to ‘FFD definition Y must not be FD .on any proper subset of X, but here City is FD in one subset .of X i.e. Sno, so City is not FFD on (Sno, Status)
Consider another case of SP table:
Here, Qty is FD on combination of Sno, Pno.
(Sno, Pno) Qty
X Y
Here, X has two proper subsets Sno and Pna
Qty is not FD on Sno, because one Sna can supply mare than .one quantity.
Qty is also not FD on Pno, because .one Pna may be supplied many times by different suppliers with different .or same quantities.
So, Qty is FFD and composite attribute of (Sno, Pno) à Qty.
Other Functional Dependencies
There are same rather types of functional dependencies, which play a vital rule during the process .of normalization of data.
Candidate Functional Dependency
A candidate functional dependency is a functional dependency that includes all attributes of the table. It should also be noted that a well-fanned dependency diagram must have at least one candidate functional dependency, and that there can be more than .one candidate functional dependency for a given dependency diagram.
Primary Functional Dependency
A primary functional dependency is a candidate functional dependency that is selected to determine the primary key. The determinant of the primary functional dependency is the primary key of the relational database table. Each dependency diagram must have one and only on primary functional dependency. If a relational database table has .only .one candidate functional dependency, then it automatically becomes the primary functional dependency
Once the primary key has been determined, there will be three possible types of functional dependencies:
Description
A → B A key attribute functionally determines a non-key attribute.
A → B A non-key attribute functionally determines a non-key attribute.
A → B A non-key attribute functionally determines a key attribute.
A partial functional dependency is a functional dependency where the determinant consists of key attributes, but not the entire primary key, and the determined consist ~ of non-key attributes.
A transitive functional dependency is a functional dependency where the determinant consists of non-key attributes and the determined also consists of non-key attributes.
A Boyce-Codd functional dependency is a functional dependency where the determinant consists of non-key attributes and the determined consists of key attributes.
A Multi-Value Dependency (MVD) occurs when two or more independent multi valued facts about the same attribute occur within the same table. It means that if in a relation R having A, Band C as attributes, B and Care multi-value facts about A, which is represented as A ààB and A ààC ,then multi value dependency exist only if B and C are independent on each other.
A Join Dependency exists if a relation R is equal to the join of the projections X Z. where X, Y, Z projections of R.
Closure of set of dependencies
Let a relation R have some functional dependencies F specified. The closure of F (usually written as F+) is the set of all functional dependencies that may be logically derived from F. Often F is the set of most obvious and important functional dependencies and. F+, the closure, is the set of all the functional dependencies including F and those that can be deduced from F. The closure is important and may, for example, be needed in finding one or more candidate keys of the relation.
For example, the student relation has the following functional dependencies
sno Sname
cno came
sno address
cno instructor
Instructor office
Let these dependencies be denoted by F. The closure of F, denoted by F +, includes F and all functional- dependencies that are implied by F.
To determine F+, we need rules for deriving all functional dependencies that are implied: by F. A set of rules that may be used to infer additional dependencies was proposed by Armstrong in 1974. These rules (or axioms) are a complete set of rules in· that all possible functional dependencies may be derived from them. The rules are:
1. Reflexivity Rule – If X is a set of attributes and Y is a subset of X, then X →Y holds.
The reflexivity rule is the simplest (almost trivial) rule. It states that each subset of X is functionally dependent on X. In other words trivial dependence is defined as follows:
Trivial functional dependency: A trivial functional dependency is a functional dependency of an attribute on a superset of itself.
For example: {Employee ID, Employee Address} → {Employee Address} is trivial, here {Employee Address} is a subset of {Employee ID, Employee Address}.
2. Augmentation Rule – If X → Y holds and W is a set of attributes, and then WX → WY holds.
The argumentation (‘u rule is also quite simple. It states that if Y is determined by X then a set of attributes W and Y together will be determined by W and X together. Note that we use the notation WX to mean the collection of all attributes in W and X and write WX rather than the more conventional (W, X) for convenience.
For example: Rno – Name; Class and Marks is a set of attributes and act as
W. Then· {Rno, Class, Marks} -> {Name, Class, Marks}
3. Transitivity Rule – If X → Y and Y → Z hold, then X → Z holds.
The transitivity rule is perhaps the most important one. It states that if X functionally determines Y and Y functionally determine Z then X functionally determines Z.
For example: Rno → City and City → Status, then Rno → Status should be holding true.
These rules are called Armstrong’s Axioms.
Further axioms may be derived from the above although the above three axioms are sound and complete in that they do not generate any incorrect functional dependencies (soundness) and they do generate all possible functional dependencies that can be inferred from F (completeness). The most important additional axioms are:
1. Union Rule – If X → Y and X → Z hold, then X → YZ holds.
2. Decomposition Rule – If X → YZ holds, then so do X → Y and X → Z.
3. Pseudo-transitivity Rule – If X → Y and WY → Z hold then so does WX → Z.
Based on the above axioms and the .functional dependencies specified for relation student, we may write a large number of functional dependencies. Some of these are:
( sno, cno) a sno (Rule 1)
(sno, cno) → cno (Rule 1)
(sno, cno) → (Sname, cname) (Rule 2)
cno → office (Rule 3)
sno → (Sname, address) (Union Rule)
Etc.
Often a very large list of dependencies can be derived from a given set F since Rule 1 itself will lead to a large number of dependencies. Since we have seven attributes (sno, Sname, address, cno, cname, instructor, office), there are 128 (that is, 2^7) subsets of these attributes. These 128 subsets could form 128 values of X in functional dependencies of the type X ~ Y. Of course, each value of X will then be associated with a number of values for Y (Y being a subset of x) Leading to several thousand dependencies. These large numbers of dependencies are not particularly helpful in achieving our aim of normalizing relations.
Although we could follow the present procedure and compute the closure of F to find all the functional dependencies, the computation requires exponential time and the list of dependencies is often very large and therefore not very useful. There are two possible approaches that can be taken to avoid dealing with the large number of dependencies in the closure. ‘One’ is to deal with one attribute or a set of attributes at a time and find its closure (i.e. all functional dependencies relating to them). The aim of this exercise is to find what attributes depend on a given set of attributes and therefore ought to be together. The other approach is to find the minimal· covers.
Minimal Functional Dependencies or Irreducible Set of Dependencies
In discussing the concept of equivalent FDs, it is useful to define the concept of minimal functional dependencies or minimal cover which is useful in eliminating necessary functional dependencies so that only the minimal numbers of dependencies need to be enforced by the system. The concept of minimal cover of F is sometimes called irreducible Set of F.
A functional depending set S is irreducible if the set has three following properties:
Each right set of a functional dependency of S contains only one attribute.
Each left set of a functional dependency of S is irreducible. It means that reducing anyone attribute from left set will change the content of S (S will lose some information).
Reducing any functional dependency will change the content of S.
Sets of functional dependencies with these properties are also called canonical or minimal.
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular