C Program for GCD of Two Integers using Euclid’s algorithm

The Greatest Common Divisor of two positive integers can be calculated iteratively by the following formula known as Euclid’s algorithm. You can see that this is a recursive definition with GCD(m,n) defined in terms of GCD(n,m%n).

                GCD(m,n)           = GCD (n,m)                      if n>m

                                              =m,                                      if n=0

                                              = GCD(n, m%n)                otherwise

We can also compute the Least Common Multiple of the two integers by using the following relation between the GCD and the LCM.

                LCM * GCD = m * n

The C program given below uses Euclid’s algorithm to compute the GCD and the LCM of two integers.

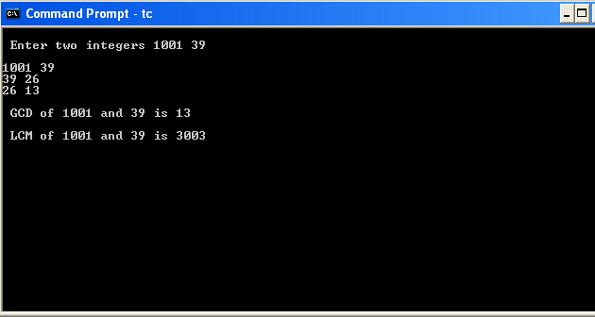
#include<stdio.h> 
 #include<stdlib.h> 
 int main() 
 { 
    long n, m, temp, big, small; 
    long gcd , lcm; 
    clrscr(); 
    printf("\n Enter two integers "); 
    scanf("%ld %ld", &n , &m); 
     if(n==0||m==0) 
     { 
                printf("\n ERROR: one of the values equals O."); 
                exit(0); 
     } 
    big=n; 
    small=m; 
      while(small!=0) 
      { 
                if(big<small) 
                { 
                   temp=big; 
                   big=small; 
                   small=temp; 
                } 
                          printf("\n %ld %ld", big , small); 
                          temp=big%small; 
                          big=small; 
                          small=temp; 
      } 
              gcd=big; 
              lcm=m*(n/big); 
              printf("\n\n GCD of %ld and %ld is %ld\n", n , m, gcd); 
              printf("\n LCM of %ld and %ld is %ld\n", n , m , lcm); 
              return 0; 
 }