The trigonometric and hyperbolic functions provided in the standard mathematical library are listed in Table. Except for the atan2 function, which takes two arguments, all other functions take a single argument and each function returns a single value. Note that the function parameters and return values are of type double.
The sin, cos and tan functions are used for the evaluation of sine, cosine and tangent, respectively, of a given angle, which must be specified in radians.
The asin, acos and atan functions return arc sine (i. e., sin-1), arc cosine (i. e., cos-1) and arc tangent (i.e., tan-1), respectively. The function call atan2 (y, x) returns the arc tangent of y/x. The angle returned by these functions is in radians. Note that the argument of the asin and acos functions must be in the range -1.0 to 1.0, both inclusive; otherwise, they give domain error. Similarly, the argument of atan function must be in the range -π/2 to π/2. The functions sinh, cosh and tanh are used to calculate the hyperbolic sine, hyperbolic cosine and hyperbolic tangent, respectively.
Table Trigonometric and hyperbolic functions in the standard library of the C language
Function Name | Typical call | Explanation | Function prototype |
sin | sin(x) | sine of x | double sin(double x) |
cos | cos (x) | cosine of x | double cos(double x) |
tan | tan(x) | tangent of x | double tan(double x) |
asin | asin(x) | sin-1(x) in range [-π/2,π/2],x∑[-1, 1] | Double asin(double x) |
acos | acos(x) | cos-1(x) in range[0,π], x ∑ [-1, 1] | double acos(double x) |
atan | atan(x) | tan-1(x) in range [-π/2, π/2] | double atan(double x) |
atan2 | atan2 (y, x) | tan–1 (y/x) in range [-π,π] | double atan2(double y, double x) |
sinh | sinh (x) | hyperbolic sine of x | double sinh(double x) |
cosh | cosh(x) | hyperbolic cosine of x | double cosh(double x) |
tanh | tanh(x) | hyperbolic tangent of x | double tanh(double x) |
While using functions in this group, we may have to convert the angles between degrees and radians. These conversions are given as θr=(π/180) θd and θd=(180/π)θr, where θd and θr are angles in degrees and radians, respectively.
Illustrates evaluation of trigonometric functions
#include <stdio.h>
#include <math.h>
int main ()
{
int A, i ;
double pi = 3.14159, C,S,T,ARad, theta;
clrscr();
printf("Angle A\t\tcos(A)\t\tsin(A)\t\ttan(A)\ndegrees\n");
for ( i =0; i<4; i++)
{
A = 60*i;
ARad = A*pi/180; //converting angle from degrees to radians.
C =cos (ARad); //calling trigonometric functions
T = tan (ARad);
S = sin (ARad);
printf("%d\t\t%4.3lf,\t\t%4.3lf\t\t%4.3lf\n",A, C,S,T);
}
theta= asin(.5)*180/pi; // conversion of radians into degrees
printf("sin inverse of .5 = % 3.3lf degrees\n", theta);
return 0;
}
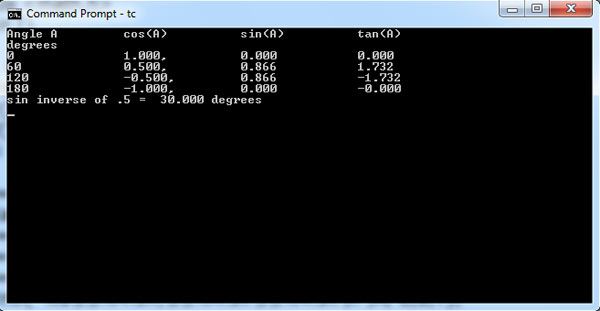
The output of sine, cosine, and tangent of different values of angle are given in tabular form. For evaluation of functions sin(), cos(), etc. the angle should be converted into radians. The return values of inverse trigonometric functions such as acos(), asin(), etc., are also in radians. These values may be converted into degrees if so needed. In the above results sin-1(.5) is evaluated in radians and converted to 30 degrees. However, if it is put as asin(l/2) the result may come out to be 0.0 because 1/2 is integer division with value 0.
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular