The purpose of error control is to ensure that the information received by the receiver is exactly the information transmitted by the sender. As the communication channel is highly unreliable, the receiver must be able to deal with the received data, if it contains error. The term error control is defined as the process of identification or correction of error occurred in the transmitted data. There are two types of error control mechanisms. They are:
Forward error control Additional redundant information is transmitted along with the useful data. Hence, the receiver not only detects the error, but also determines the location of the error in the data. This method is not widely used, because of the number of additional redundant information.
Feedback or (backward) error control Along with each character, little additional information is added only for error detection. The receiver performs no error correction. If the received data contains error, then the entire data is retransmitted. Hence, the feedback techniques perform error detection and retransmission.
Error detection There are different error detection schemes used. The type of detection scheme depends on the type of error and the type of transmission (synchronous or asynchronous) also. There are random single bit errors in asynchronous or synchronous mode of transmission and burst error occurs in a group of continuous bits. The most widely used error-detecting codes are the parity, block sum check, and the cyclic redundancy check (CRC) codes.
Parity The most common method of detecting the errors is the use of parity. With this method, the bits of a character to be transmitted are inspected and an extra bit is added before the transmission. This bit is known as the parity bit. The bit is chosen to be a ‘0’ or a ‘1’, in order to keep the total number of ‘1’ s ‘1’ bits in the character odd or even respectively. To compute the parity bit, the number of bits in the character is added first, using modulo-2 addition, the result may be a ‘0’ or a ‘1’. If the parity is chosen as odd, then the additional bit added must make the result into a ‘1’ if the parity chosen is even, then the additional bit must make the result into a ‘0’. Following is an example for the parity generation. 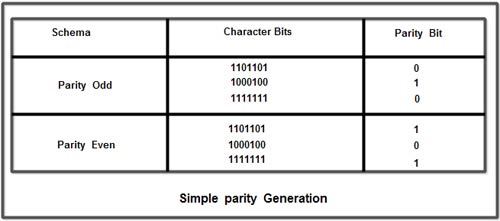 At the receiving end, after the reception of the character, the parity bit is removed from the received character. The remaining bits are added using the modulo-2 addition and the result is checked with the received parity bit. If these two values differ, then the received character contains an error. Hence the use of parity bit is to detect single bit errors.
At the receiving end, after the reception of the character, the parity bit is removed from the received character. The remaining bits are added using the modulo-2 addition and the result is checked with the received parity bit. If these two values differ, then the received character contains an error. Hence the use of parity bit is to detect single bit errors.
Block error control When a burst of characters is transmitted, there may be possibilities for single bit or multiple bit error that leads to retransmission of the whole block of characters. Hence, it is necessary to use error-detecting techniques to find out the occurrence of error in the block. The parity method discussed earlier can be extended to a block of data also. A block of character is called as frame. The frame contains one additional column and one additional row. By generating the parity bit for each individual character, the column is created. The last row of the frame is formed by finding the parity bit for each bit position. A sample frame with row and column parity is shown below.
The main advantage of this scheme is the detection of two-bit error. As a simple parity bit can detect only single bit error. If two-bit changes occur in the transmitted data, the resultant parity bit is same as the parity of the transmitted character. In the above scheme, if a two-bit error occurs in a transmitted character, the received parity bit remains the same. But these two bit errors change the column parity at the receiver. Hence, the receiver can identify two-bit errors. But simultaneous occurrence of two-bit errors in two characters at the same column positions can be unnoticed by the receiver. Clearly, the probability of this occurring is much less than the probability of two-bit errors.
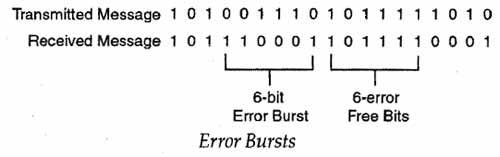
The simple parity and block sum check methods are well suited for applications in which random single bit errors are present. More precautionary measures; are to be taken to control continuous error burst. An error burst is defined as the number of bits between two successive error bits, including the two incorrect bits. The length of the error burst is determined from the number B, the difference between the last erroneous bit in a burst and the first erroneous bit of the next burst. In this case, B correct bits separate the two bursts. The following figure illustrates the error bursts that occur in the transmitted sequence of bits.
 Parity or block sum check does not provide a reliable error detection scheme for burst error. A new technique called polynomial codes are used for the identification of errors. Along with each block of data transmitted, a single set of check-digits are also transmitted. The check – digits are generated based on a predefined method of computation. At the receiver, the same computation is again performed with the received set of data, and the results are compared with the received check digits. If both the computed and the received check digits match, then there is no error in the transmission. On the other hand, if they differ, then it is considered as an error in the transmission. The computed check digits are known as frame check sequence or cyclic redundancy check (CRC) digits. Following section gives details of CRC codes.
Parity or block sum check does not provide a reliable error detection scheme for burst error. A new technique called polynomial codes are used for the identification of errors. Along with each block of data transmitted, a single set of check-digits are also transmitted. The check – digits are generated based on a predefined method of computation. At the receiver, the same computation is again performed with the received set of data, and the results are compared with the received check digits. If both the computed and the received check digits match, then there is no error in the transmission. On the other hand, if they differ, then it is considered as an error in the transmission. The computed check digits are known as frame check sequence or cyclic redundancy check (CRC) digits. Following section gives details of CRC codes.
Cyclic Redundancy Check (CRC) CRC is the most widely used error – detecting method alternative to the simple parity check codes. Instead of adding the number of bits to obtain the desired parity, in CRC a sequence of ‘extra’ redundant bits are added at the end of data. These bits are known as CRC bits. The CRC bits are derived from the original data bits. The method of deriving the CRC bits at the sending side is given below:
Step 1: A sequence of bit stream is formed by appending n ‘0’ bits to the data at the end.
Step 2: A predetermined devisor of length n+ 1 bits is used to divide the sequence and the remainder is calculated. The remainder is known as CRC.
Step 3: The remainder replaces the extra bits added to the data at the beginning.
Step 4: The combined sequence of data plus CRC is transmitted by the sender.
At the receiving end the received data plus CRC is again divided by the same divisor as used at the sending side. If the remainder is zero then it is presumed that the data is error – free and the receiver accepts the data, on the other hand if the remainder is non-zero, the data is considered as corrupted and the received data is discarded. For example, consider the 6-bit data sequence “100110”. Let us choose a 3-bit divisor 110at the sending side. As per the step 1, two 0s are added to the data sequence and the new sequence is “10011000”. As per the second step, the new sequence is divided by 110 (Modulo-2 division is used), and produces a remainder of 10. This is the CRC. As stated in step 3, this CRC code is added to the data sequence to produce a sequence “10011010” and then transmitted.
At the receiver side, if the received sequence does not contain an error, the sequence “10011010” is again divided by the same divisor 110 and the remainder is 00. If an error is made in one or two bits (corrupted), then the remainder will not be a 00, hence, the receiver rejects the data.
Checksum Another method of error detection, often used in higher order layers is checksum.
Checksum is computed at the sending end using the following steps.
Step 1: The data sequence is divided into ‘K’ words of same size n (8 or 16 bits).
Step 2: All words are added using l’s complement addition and the sum is computed.
Step 3: The l’s complement of the sum, known as checksum is transmitted with the data.
At the receiver side, the following steps are carried out after receiving the data with checksum
Step 1: The data sequence is divided into ‘K+1’ words of same size ‘n’ (8 or 16 bits).
Step 2: All words are added using l’s complement addition and the sum is computed.
Step 3: The sum is complemented, if it is 0, the data is error – free and is accepted; otherwise the received data is discarded.
Error correcting codes Techniques covered so far deal with error detection only. When error detecting techniques are used, and the receiver receives the data with error, the receiver discards the data and asks for retransmission. On the other hand, error-correcting codes are used to identify the error bits in the received data and correct them. The main problem with error-correcting codes is that they require more redundancy bits than the error-detecting codes. This leads to wastage of transmission bandwidth.
Single-bit error correction The key issue in error-correction is to identify the position of invalid error bit, in order to correct it. For example, when 7-bit ASCII code is transmitted, the error-correcting code must identify the position of the bit that contains an error. Hence, at least three redundant bits are used to identify the possibility of error in the seven positions in an ASCII character. However, if an error occurs at the redundant bits themselves, to identify it, additional bits are required. Hence the total number of bits in the transmitted data contains m+k bits. M is the number of message bits and K is the number of redundant bits.
The calculation of the total number of redundant bits for single bit error correction is straightforward. One bit is used for ensuring that the received data is error-free. Other bits are used to indicate one out of M message and K redundant bits that may contain an error. Hence, the value of K must be chosen such that 2K <: M+K+ 1. For example to correct single bit error in 7-bit ASCII code, at least 4 redundant bits are needed. Hence, the transmitted data contains 11bits for each data units.
Hamming codes RW. Hamming illustrated the concept of hamming distance, which is useful in considering the properties of codes. Hamming distance is defined as the number of bit positions by which two states differ from each other. This parameter is very useful for error-detection and correction. Hamming introduced a code for single bit error correction by inserting multiple parity check bits at selected positions of data before transmission. The receiver recalculates the check – bits, compares it with the received check – bits, and determines the error bit. For 4~bitcode three check – bits are required for error-correction as shown in Figure.
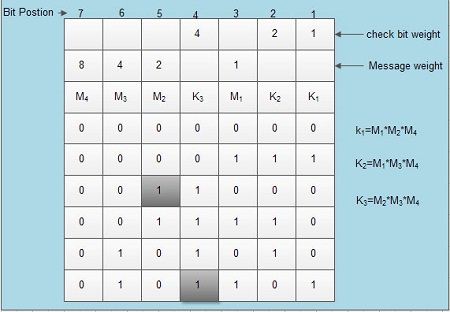 Modulo-2 addition is used for the formation of the K redundant check bits. If any of the message bit is corrupt, then the received check bits may appear as incorrect. For example if the message bit M2 of the third message unit is incorrect (see the encircled bit of the third row), it appears as 0 instead of 1. In this case, the receiver calculates the check bits K1and K3as 0 and 0 respectively instead of 1, 1 as it is now. The position of the error bit is computed by simply adding the weights of K1 (1) and K3 (4) that is 4+1=5, hence, bit at position 5, that isM2 is the error bit. Similarly, if anyone of the check bit is invalid (see the encircled bit of the last row), its weight indicates the position of the error bit (4 in this case). Hence hamming codes can be much useful to perform single bit error correction. For double bit and 3-bit errors the number of redundant bits required is more than that of the message size.
Modulo-2 addition is used for the formation of the K redundant check bits. If any of the message bit is corrupt, then the received check bits may appear as incorrect. For example if the message bit M2 of the third message unit is incorrect (see the encircled bit of the third row), it appears as 0 instead of 1. In this case, the receiver calculates the check bits K1and K3as 0 and 0 respectively instead of 1, 1 as it is now. The position of the error bit is computed by simply adding the weights of K1 (1) and K3 (4) that is 4+1=5, hence, bit at position 5, that isM2 is the error bit. Similarly, if anyone of the check bit is invalid (see the encircled bit of the last row), its weight indicates the position of the error bit (4 in this case). Hence hamming codes can be much useful to perform single bit error correction. For double bit and 3-bit errors the number of redundant bits required is more than that of the message size.
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular