DDA algorithm is an incremental scan conversion method. Here we perform calculations at each step using the results from the preceding step. The characteristic of the DDA algorithm is to take unit steps along one coordinate and compute the corresponding values along the other coordinate. The unit steps are always along the coordinate of greatest change, e.g. if dx = 10 and dy = 5, then we would take unit steps along x and compute the steps along y.
Suppose at step i we have calculated (xi, yi) to be a point on the line. Since the next point (x i+1,y i+1) should satisfy ?y/? x =m where ?y= y i+1–yi and ? x= x i+1–xi , we have y i+1= yi + m? x or x i+1=xi+ ? y/m
These formulas are used in DDA algorithm as follows. When |m| ? 1, we start with x = x1’? (assuming that x1’ <x2’) and y = y1’, and set ? x =1( i.e., unit increment in the x direction). The y coordinate of each successive point on the line is calculated using y i+1= yi + m.
When |m| >1, we start with x= x1’ and y= y1’ (assuming that y1’ < y2’), set ? y =1 ( i.e., unit increment in the y direction). The x coordinate of each successive point on the line is calculated using x i+1=xi+ 1/m. This process continues until x reaches x2’(for m| ? 1 case )or y reaches y2’ (for m| > 1 case ) and all points are scan converted to pixel points.
The explanation is as follows: In DDA algorithm we have to find the new point xi+1 and yi+1 from the existing points xi and yi. As a first step here we identify the major axis and the minor axis of the line to be drawn. Once the major axis is found we sample the major axis at unit intervals and find the value in the other axis by using the slope equation of the line.
For example if the end points of the line is given as (x1,y1)= (2,2) and (x2, y2)= (9,5). Here we will calculate y2-y1 and x2-x1 to find which one is greater. Here y2-y1 =3 and x2-x1 =7; therefore here the major axis is the x axis. So here we need to sample the x axis at unit intervals i.e.? x = 1 and we will find out the y values for each ? x in the x axis using the slope equation.
In DDA we need to consider two cases; one is slope of the line less than or equal to one (|m| ? 1)and slope of the line greater than one (m| > 1). When |m| ? 1 means y2-y1 = x2-x1 or y2-y1 <x2-x1.In both these cases we assume x to be the major axis. Therefore we sample x axis at unit intervals and find the y values corresponding to each x value.
We have the slope equation as
? y = m ? x
y2-y1 = m (x2-x1)
In general terms we can say that y i+1 – yi = m(x i+1 – xi ). But here ? x = 1; therefore the equation reduces to y i+1= yi + m = yi + dy/dx.
When m| > 1 means y2-y1> x2-x1 and therefore we assume y to be the major axis. Here
we sample y axis at unit intervals and find the x values corresponding to each y value. We have the slope equation as
? y = m ? x
y2-y1 = m (x2-x1)
In general terms we can say that y i+1 – yi = m(x i+1 – xi ). But here ? y = 1; therefore the equation reduces to 1 = m(x i+1 – xi). Therefore
x i+1=xi+ 1/m
x i+1=xi+ dx/dy
DDA Algorithm is given below:
procedure DDA( x1, y1, x2, y2: integer);
var
dx, dy, steps: integer;
x_inc, y_inc, x, y: real;
begin
dx := x2 – x1; dy := y2 – y1;
if abs(dx) > abs(dy) then
steps := abs(dx); {steps is larger of dx, dy}
else
steps := abs(dy);
x_inc := dx/steps; y_inc := dy/steps;
{either x_inc or y_inc = 1.0, the other is the slope}
x:=x1; y:=y1;
set_pixel(round(x), round(y));
for i := 1 to steps do
begin
x := x + x_inc;
y := y + y_inc;
set_pixel(round(x), round(y));
end;
end; {DDA}
The DDA algorithm is faster than the direct use of the line equation since it calculates points on the line without any floating point multiplication.
Advantages of DDA Algorithm
1. It is the simplest algorithm and it does not require special skills for implementation.
2. It is a faster method for calculating pixel positions than the direct use of equation y = mx + b. It eliminates the multiplication in the equation by making use of raster characteristics, so that appropriate increments are applied in the x or v direction to find the pixel positions along the line path.
Disadvantages of DDAAlgorithm
1. Floating point arithmetic in DDA algorithm is still time-consuming.
2. The algorithm is orientation dependent. Hence end point accuracy is poor.
Let us see few examples to illustrate this algorithm.
Consider the line from (0,0) to (4,6). Use the simple DDA algorithm to rasterize this line.
Sol. Evaluating steps 1 to 5 in the DDA algorithm we have
Xl = 0 Y1 = 0
X2 = 4 Y2 = 6
Length = |Y2-Y1l = 6
∆X = |X2– Xl | / Length
= 4
6
∆Y = |Y2– Yl | / Length
= 6/6=1
Initial value for
X = 0 + 0.5 * Sign (4) = 0.5
6
Y = 0 + 0.5 * Sign (1) = 0.5
Tabulating the results of each iteration in the step 6 we get,
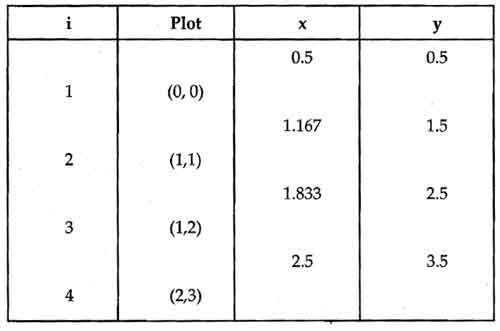

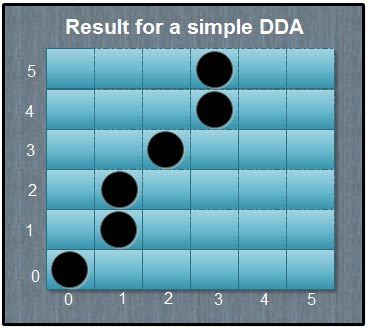
The results are plotted as shown in the Fig. It shows that the rasterized line lies to both sides of the actual line, i.e. the algorithm is orientation dependent.
Example 2 Consider the line from (0, 0) to (-6, -6). Use the simple DDA algorithm line.
Sol. Evaluating steps 1 to 5 in the DDA algorithm we have
Xl = 0 Y1 = 0
X2 = – 6 Y2 = – 6
Length = l X2-X1l |Y2-Y1l = 6
∆X = ∆Y = -1
Initial values for
X = 0 + 0.5 * Sign (-1) =-0.5
Y = 0 + 0.5 * Sign (-1) =-0.5
Tabulating the results of each iteration in the step 6 we get,
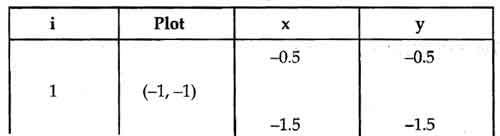

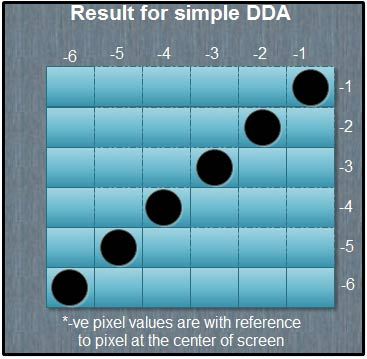
The results are plotted as shown in the Fig. It shows that the rasterized line lies on the actual line and it is 45° line.
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular