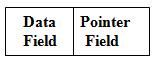
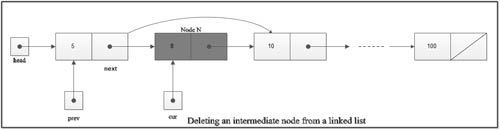
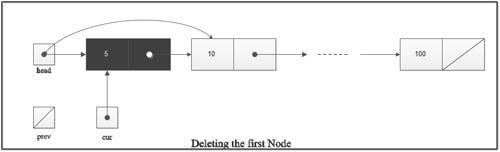
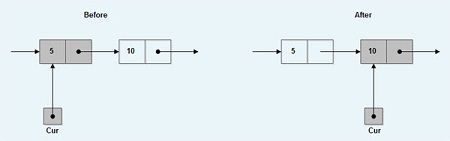
The function free() is used to de-allocate the memory allocated by the functions malloc ( ), calloc ( ), etc, and return it to heap so that it can be used for other purposes. The argument of the function free ( ) is the pointer to the memory which is to be freed. The prototype of the function is as below.
void free(void *ptr);
When free () is used for freeing memory allocated by malloc () or realloc (),the whole allocated memory block is released. For the memory allocated by function calloc () also all the segments of memory allocated by calloc () are de-allocated by free (). This is illustrated by Program. The following program demonstrates the use of function calloc () and the action of function free () on the memories allocated by calloc () .
Illustrates that function free () frees all blocks of memory allocated by calloc () function
#include <stdio.h>
#include<stdlib.h>
main()
{
int i,j,k, n ;
int* Array;
clrscr();
printf("Enter the number of elements of Array : ");
scanf("%d", &n );
Array= (int*) calloc(n, sizeof(int));
if( Array== (int*)NULL)
{
printf("Error. Out of memory.\n");
exit (0);
}
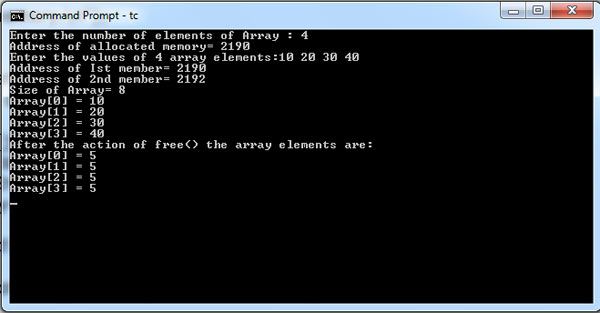
printf("Address of allocated memory= %u\n" , Array);
printf("Enter the values of %d array elements:", n);
for (j =0; j<n; j++)
scanf("%d",&Array[j]);
printf("Address of Ist member= %u\n", Array);
printf("Address of 2nd member= %u\n", Array+1);
printf("Size of Array= %u\n", n* sizeof(int) );
for ( i = 0 ; i<n; i++)
printf("Array[%d] = %d\n", i, *(Array+i));
free(Array);
printf("After the action of free() the array elements are:\n");
for (k =0;k<n; k++)
printf("Array[%d] = %d\n", k, *(Array+i));
return 0;
}