Digital data is represented, stored and transmitted as groups of binary digits also known as binary code. The binary codes can be classified as shown in Fig.
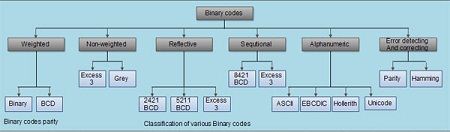
Weighted codes: In weighted codes, each digit is assigned a specific weight according to its position. For example, in 8421BCD code, 1001 the weights of 1, 0, 0, 1 (from left to right) are 8, 4, 2 and 1 respectively.
Suppose W1‘ W2‘ W3 and W4 are the weights of binary digits and Xl‘ X2, X3 and X4 are the corresponding digit values then decimal digit. N = W1 Xl + W2 X2 + W3 X3 + W4 X4 is represented by binary sequence X4 X3 X2 X4.
The codes 8421BCD, 2421BCD, 5211BCD are all weighted codes.
• Non-weighted codes: The non-weighted codes are not positionally weighted. In other words, each digit position within the number is not assigned a fixed value ( or weight ).
Excess-3 and gray code are non-weighted codes.
• Reflective codes: A code is reflective when the code is self complementing. In other words, when the code for 9 is the complement the code for 0, 8 for 1, 7 for 2, 6 for 3 and 5 for 4.
2421BCD, 5421BCD and Excess-3 code are reflective codes.
• Sequential codes: In sequential codes, each succeeding ‘code is one binary number greater than its preceding code. This property helps in manipulation of data.
8421 BCD and Excess-3 are sequential codes.
• Alphanumeric codes: Codes used to represent numbers, alphabetic characters, symbols and various instructions necessary for conveying intelligible information.
ASCII, EBCDIC, UNICODE are the most-commonly used alphanumeric codes.
• Error defecting and correcting codes: Codes which allow error defection and correction are called error detecting and’ correcting codes. Hamming code is the mostly commonly used error detecting and correcting code.
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular