Excess-3 Code (XS3)

Excess-3, also called XS3, is a non-weighted code used to express decimal number-s. It is another important binary code. It is particularly significant for arithmetic operations as it overcomes the shortcomings encountered while using the 8421 BCD code to add two decimal digits whose sum exceeds 9. This code is used in some old computers.

The Excess-3 code for a given decimal number is determined by adding ‘3’ to each decimal digit in the given number and then replacing each digit of the newly found decimal number by its four bit binary equivalent. The table gives is the Excess-3 code. For example, XS3 code of 24 is obtained as

  2       4

+3    +3

  5       7

0101 0111

Thus, XS3 code of 24 is 0101 0111.

The key feature of the Excess-3 code is .that it is self complementing. In other words, the l’s complement of an Excess- 3 number is the Excess- 3 code for the 9’s complement of the corresponding decimal number. For example, the Excess- 3 code for decimal 6 is 1001. The l’s complement of 1001 is 0110, which is the Excess-3 code for decimal 3, and 3 is the 9’s complement of 6. This property of Excess-3 code makes it useful in some arithmetic operations.

Now let us consider a few examples. The Excess-3 code for decimal number 27 is 01011010.

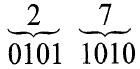
Similarly, Excess-3 code for (597)₁₀ and (14.57)₁₀ is

(597)₁₀ = (100011001010)

(14.57)₁₀ = (01000111.10001010)

One should note that corresponding to given Excess-3 code, the equivalent decimal number can be determined by first splitting the number into four-bit groups, starting from radix point and then subtracting 0011 from each four-bit group. This gives us 8421 BCD equivalent of the given Excess-3 code, which can then be converted into the equivalent decimal number. For example; Let us suppose we want to determine the decimal equivalent for the Excess-3 code 1000110. First we make group of 4 bits starting from radix point.

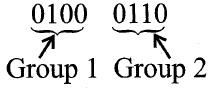
Subtracting 0011 from each group, we obtain the new number as 00010011. Its decimal equivalent is 13.

Therefore, (1000110) Excess-3= (13)₁₀