Regular expression is used to represent the language (lexeme) of finite automata (lexical analyzer).
We’ll be covering the following topics in this tutorial:
Finite automata
A recognizer for a language is a program that takes as input a string x and answers yes if x is a sentence of the language and no otherwise.
A regular expression is compiled into a recognizer by constructing a generalized transition diagram called a Finite Automaton (FA).
Finite automata can be Non-deterministic Finite Automata (NFA) or Deterministic Finite Automata (DFA).
It is given by M = (Q, Σ, qo, F, δ).
Where Q – Set of states
Σ – Set of input symbols
qo – Start state
F – set of final states
δ – Transition function (mapping states to input symbol).
δ :Q x Σ → Q
• Non-deterministic Finite Automata (NFA)
o More than one transition occurs for any input symbol from a state.
o Transition can occur even on empty string (Ɛ).
• Deterministic Finite Automata (DFA)
o For each state and for each input symbol, exactly one transition occurs from that state.
Regular expression can be converted into DFA by the following methods:
(i) Thompson’s subset construction
• Given regular expression is converted into NFA
• Resultant NFA is converted into DFA
(ii) Direct Method
• In direct method, given regular expression is converted directly into DFA.
Rules for Conversion of Regular Expression to NFA
• Union
r = r1 + r2
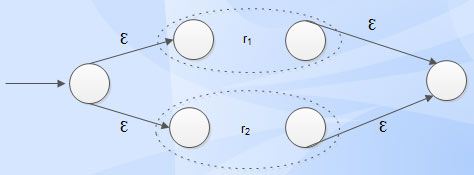
Concatenation
r = r1 r2

Closure
r = r1*

Ɛ –closure
Ɛ – Closure is the set of states that are reachable from the state concerned on taking empty string as input. It describes the path that consumes empty string (Ɛ) to reach some states of NFA.
Example 1
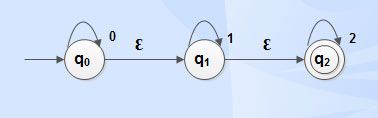
Ɛ -closure(q0) = { q0, q1, q2}
Ɛ –closure(q1 ) = {q1, q2}
Ɛ -closure(q2) = { q0}
Example 2
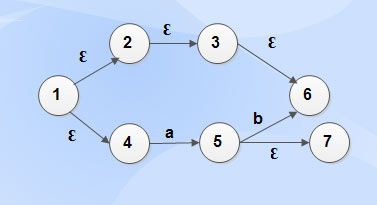
Ɛ -closure (l) = {l, 2, 3, 4, 6}
Ɛ-closure (2) = {2, 3, 6}
Ɛ-closure (3) = {3, 6}
Ɛ-closure (4) = {4}
Ɛ-closure (5) = {5, 7}
Ɛ -closure (6) = {6}
Ɛ-closure (7) = {7}
Sub-set Construction
• Given regular expression is converted into NFA.
• Then, NFA is converted into DFA.
Steps
l. Convert into NFA using above rules for operators (union, concatenation and closure) and precedence.
2. Find Ɛ -closure of all states.
3. Start with epsilon closure of start state of NFA.
4. Apply the input symbols and find its epsilon closure.
Dtran[state, input symbol] = Ɛ -closure(move(state, input symbol))
where Dtran àtransition function of DFA
5. Analyze the output state to find whether it is a new state.
6. If new state is found, repeat step 4 and step 5 until no more new states are found.
7. Construct the transition table for Dtran function.
8. Draw the transition diagram with start state as the Ɛ -closure (start state of NFA) and final state is the state that contains final state of NFA drawn.
Direct Method
• Direct method is used to convert given regular expression directly into DFA.
• Uses augmented regular expression r#.
• Important states of NFA correspond to positions in regular expression that hold symbols of the alphabet.
Regular expression is represented as syntax tree where interior nodes correspond to operators representing union, concatenation and closure operations.
• Leaf nodes corresponds to the input symbols
• Construct DFA directly from a regular expression by computing the functions nullable(n), firstpos(n), lastpos(n) andfollowpos(i) from the syntax tree.
o nullable (n): Is true for * node and node labeled with Ɛ. For other nodes it is false.
o firstpos (n): Set of positions at node ti that corresponds to the first symbol of the sub-expression rooted at n.
o lastpos (n): Set of positions at node ti that corresponds to the last symbol of the sub-expression rooted at n.
o followpos (i): Set of positions that follows given position by matching the first or last symbol of a string generated by sub-expression of the given regular expression.
Rules for computing nullable, firstpos and lastpos
Node n | nullable (n) | firstpos (n) | lastpos (n) |
A leaf labeled Ɛ | True | Ø | Ø |
A leaf with position i | False | {i} | {i} |
An or node n = c1| c2 | Nullable (c1 ) or Nullable (c2 ) | firstpos (c1) U firstpos (c2) | Iastpos (c1) U Iastpos (c2) |
A cat node n = c1c2 | Nullable (c1 ) and Nullable (c2 ) | If (Nullable (c1 )) firstpos (c1) U firstpos (c2) else firstpos (c1) | If (Nullable (c2 )) lastpos (c1) U Iastpos (c2) else lastpos (c1) |
A star node n = c1* | True | firstpos (c1) | lastpos (c1) |
Computation of followpos
The position of regular expression can follow another in the following ways:
• If n is a cat node with left child c1 and right child c2, then for every position i in lastpos(c1), all positions in firstpos(c2) are in followpos(i).
o For cat node, for each position i in lastpos of its left child, the firstpos of its
right child will be in followpos(i).
• If n is a star node and i is a position in lastpos(n), then all positions in firstpos(n) are in followpos(i).
o For star node, the firstpos of that node is in f ollowpos of all positions in lastpos of that node.
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular