• Regular expressions are a notation to represent lexeme patterns for a token.
• They are used to represent the language for lexical analyzer.
• They assist in finding the type of token that accounts for a particular lexeme.
We’ll be covering the following topics in this tutorial:
Strings and Languages
Alphabets are finite, non-empty set of input symbols.
Σ = {0, 1} – binary alphabets
String represents the collection of alphabets.
w = {0,1, 00, 01, 10, 11, 001, 010, … }
w indicates the set of possible strings for the given binary alphabet Σ
Language (L) is the collection of strings which are accepted by finite automata.
L = {0n1 I n >= 0}
Length of string is defined as the number of input symbols in a given string. It is found by || operator.
Let ω = 0101
| ω | =4
Empty string denotes zero occurrence of input symbol. It is represented by Ɛ. Concatenation of two strings p and q is denoted by pq.
Let p = 010
And q = 001
pq = 010001
qp = 001010
i.e., pq ≠ qp
Empty string is identity under concatenation.
Let x be a string.
Ex= XE= X
Prefix A prefix of any string s, is obtained by removing zero or more symbols from the end of s.
(eg.) s = balloon
Possible prefixes are: ball, balloon,
Suffix A suffix of any string s, is obtained by removing zero or more symbols from the beginning of s.
(eg.) s =balloon
Possible prefixes are: loon, balloon
Proper prefix: Proper prefix p of a strings, can be given by s ≠ p and p ≠ E
Proper suffix: Proper suffix x of a string s, can be given by s ≠ x and x ≠ E
Substring: Substring is part of a string obtained by removing any prefix and any suffix from s.
Operations on Languages
Important operations on a language are:
• Union
• Concatenation and
• Closure
Union
Union of two languages Land M produces the set of strings which may be either in language L or in language M or in both. It can be denoted as,
LUM = {p I p is in L or p is in M}
Concatenation
Concatenation of two languages L and M, produces a set of strings which are formed by merging the strings in L with strings in M (strings in L must be followed by strings in M). It can be represented as,
LUM= {pq | p is in L and q is in M}
Closure
Kleene closure (L*)
Kleene closure refers to zero or more occurrences of input symbols in a string, i.e., it includes empty string Ɛ(set of strings with 0 or more occurrences of input symbols).
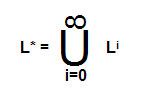
Positive closure (L +)
Positive closure indicates one or more occurrences of input symbols in a string, i.e., it excludes empty string Ɛ(set of strings with 1or more occurrences of input symbols).
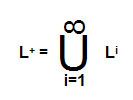
L3– set of strings each with length 3.
(eg.) Let Σ = {a, b}
L* = {E, a, b, aa, ab, ba, bb, aab, aba, aaba, … }
L+ = {a, b, aa, ab, ba, bb, aab, aaba, }
L3 = {aaa, aba, abb, bba, bob, bbb, }
Precedence of operators
• Unary operator (*) is having highest precedence.
• Concatenation operator (-) is second highest and is left associative.
letter_ (letter_ I digit )*
• Union operator ( I or U) has least precedence and is left associative.
Based on the precedence, the regular expression is transformed to finite automata when implementing lexical analyzer.
Regular Expressions
Regular expressions are a combination of input symbols and language operators such as union, concatenation and closure.
It can be used to describe the identifier for a language. The identifier is a collection of letters, digits and underscore which must begin with a letter. Hence, the regular expression for an identifier can be given by,
Letter_ (letter I digit)*
Note: Vertical bar ( I ) refers to ‘or’ (Union operator).
The following describes the language for given regular expression:
Languages for regular expressions
S.No. | Regular expression | Language |
| 1 | r | L(r) |
| 2 | a | L(a) |
| 3 | r | s | L(r) | L(s) |
| 4 | rs | L(r) L(s) |
| 5 | r* | (L(r))* |
Regular set Language defined by regular expression.
Two regular expressions are equivalent, if they represent the same regular set.
(p I q) = (q | p)
Algebraic laws of regular expressions
Law | Description |
| r | s = s | r | | is commutative |
| r | (s | t) = (r | s ) | t | | is associative |
| r (st) = (rs)t | Concatenation is associative |
| r(s|t) = rs | rt; (s|t)r = sr | tr | Concatenation is distributive |
| Ɛr = rƐ = r | Ɛ is identity for concatenation |
| r* = (r | Ɛ)* | Ɛ is guaranteed in closure |
| r** = r* | * is idempotent |
Regular Definition
Regular definition d gives aliases to regular expressions r and uses it for convenience. Sequences of definitions are of the following form
di –> ri
d2–>r2
d3–> rs
dn–> rn
in which definitions di, d2, … , can be used in place of ri, r2 respectively.
letter –> A I B I · · · I Z I a I b I · · · I z I
digit –>0 |1 I 2 … I 9
id –> letter_ (letter I digit)*
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular