Recursive Function

A recursive function is a function which invokes itself repeatedly. In this case function name appears within the function. Two examples of recursive function are given as follows:

 Example

The recursive function q finds the quotient when a is divided by b. a and b are integers.

#include <iostream.h>
int q(int a, int b) {
    if(a<b)
        return 0;
    else
        return(q(a-b,b)+1);
}
void main() {
     int a=7, b=2, ql;
     ql=q(a,b);
     cout<<"Quotient ql is : "<<ql <<"\n";
}    

When a is replaced by the value 7, following function calls will be made:

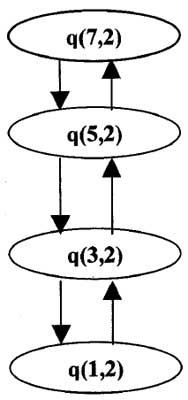
The assignment of values proceeds in the reverse direction.

q(3,2) = q(I,2) +1 = 0 + 1

q(5,2) = q(3,2) + 1 = 1+ 1

q(7,2) = q(5,2) + 1 = 2 + 1

Thus when 7 is divided by 2, the quotient is 3.

Example

Illustrates recursive function for finding greatest common divisor.

#include <iostream.h>
  int gcd(int a, int b) {
   if((a<0) || (b<0)) {
     cout<<"Error ";
     return 0;
}
else
   if(a==0)
      return b;
   else {
      return(gcd( a%b,b));
   }
}
void main() {
     int a=25, b=5, gl;
     gl=gcd(a,b);
     cout<<"gcd is : "<<gl;
}

In the above recursive function gcd, value b is returned for the greatest common divisor when a = 0.If either a or b is less than 0, the value 0 is returned to indicate an error otherwise a recursive call to the function gcd is made.

A recursive function can be written only when there is a base criterion. In the previous example, the base criterion was quotient = 0 if a<b and in the present example, the base criterion is greatest common divisor = b when a = 0.Each time the function calls itself, it gets closer and closet; to the base criterion.

Example

This is an example to illustrate that a function can call another function. It also illustrates the use of recursive function for computing the power. The program is used for evaluating the integral using Simpson’s rule. Value of an integral using Simpson’s rule is evaluated using the formula:

h/3 [f(a) + 3f(a+h) +2f(a+2h) +3f(a+3h) +2f(a+4h) +3f(a+5h) +…… +3f(a+(2n 1)h))+f(a+2nh))]

where 2n is the number of intervals, h is the step length usually chosen as a small float value <=0.2. The number of intervals over which the integration is carried out is chosen to be even. An efficient way of writing the algorithm is as follows. Various groups which can be formed are :

f(a) +3 f(a+h) + f(a+2h)

f(a+2h) +3 f(a+3h) + f(a+4h)

f(a+(2n-2)h) +3f(a+(2n-1)h) +f(a+2nh)

If there are 2n intervals, number of times the above mentioned sums have to be computed is only n. This can be seen in the for loop in the sim() function.

#include <iostream.h>
   int p1, num;
   float x, h, part, a, b;
   float f(float x) {
   float power(float, int);
   return(power(x,4)+power(x,3)+power(x,2)+ 1);
}
float power(float x, int n) {
   int i;
   if(x==0.0)
      return 0;
   else if(n==0)
      return 1;
   for(i=0;i<n;i++)
     return(power(x,n-1)+x);
}
   float sim(float x) {
   float s=0.0;
     int i;
     part = num/2;
     x=a;
     p1 =part;
     for(i=0;i<p1;i++) {
         s=s+h/3*(f(x)+3*f(x+h)+f(x+2*h));
         x=x+2*h;
     }
     return s;
  }
 void main() {
    cout<<"enter the value of x ";
    cin>>x;
    cout<<"enter the lower and upper limits of integration ";
    cout<<"\nlower";
    cin>>a;
    cout<<"\nUpper";
    cin>>b;
    cout<<"enter the number of intervals";
    cin>>num;
    h=(b-a)/num;
    cout<<"value of integral is:"<<sim(x);
}