What is Binary Search

In a linear search the search is done over the entire list even if the element to be searched is not available. Some of our improvements work to minimize the cost of traversing the whole data set, but those improvements only cover up what is really a problem with the algorithm.

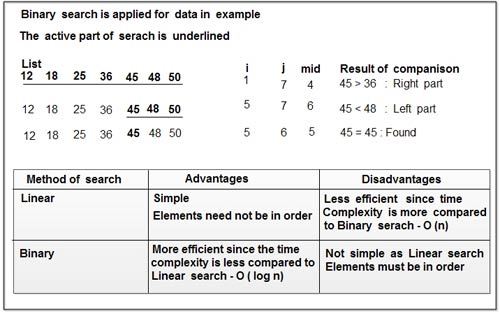
By thinking of the data in a different way, we can make speed improvements that are much better than anything linear search can guarantee. Consider a list in sorted order. It would work to search from the beginning until an item is found or the end is reached, but it makes more sense to remove as much of the working data set as possible so that the item is found more quickly.

If we started at the middle of the list we could determine which half the item is in (because the list is sorted). This effectively divides the working range in half with a single test. This in turn reduces the time complexity.

Algorithm:

bool Binary_Search ( int *list, int size, int key, int* rec )

{

bool found = false;

int low = 0, high = size – 1;

while ( high >= low )

{

int mid = ( low + high ) / 2;

if ( key < list[mid] )

high = mid – 1;

else

if ( key > list[mid] )

low = mid + 1;

else

{

found = true;

rec = &list[mid];

break;

}

}

return found;

}