This sorting technique is named so because of the logic is similar to the bubble in water. When a bubble is formed it is small at the bottom and when it moves up it becomes bigger and bigger i.e. bubbles are in ascending order of their size from the bottom to the top.
This sorting method proceeds by scanning through the elements one pair at a time, and swapping any adjacent pairs it finds to be out of order.
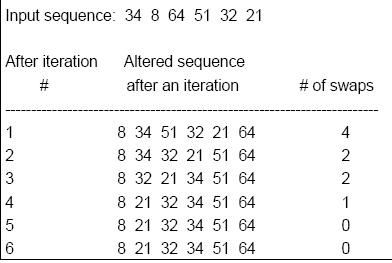
Each pass consists of comparing each element in the file with its successor (x[i] > x[i+1]) Swap the two elements if they are not in proper order. After each pass i, the largest element x[n-(i- 1)] is in its proper position within the sorted array.
Bubble Sort – Algorithm
bubble(int x[], int n)
{
int hold, j, pass;
int switched = TRUE;
for (pass = 0; pass < n – 1 && switched == TRUE; pass++)
{
switched = FALSE;
for (j = 0; j < n-pass-1; j++)
if (x[j] > x[j+1])
{
switched = TRUE; /* swap x[j], x[j+1] */
hold = x[j];
x[j] = x[j+1];
x[j+1] = hold;
}
} /* it stops if there is no swap in the pass */
}
In the first pass, n-1 items have to be scanned. On the second pass, the second largest item will move to its correct position, and on the third pass (stopping at item n-3) the third largest will be in place. It is this gradual filtration, or bubbling of the larger items to the top end that gives this sorting technique its name.
There are two ways in which the sort can terminate with everything in the right order. It could complete by reaching the n-1st pass and placing the second smallest item in its correct position.
Alternatively, it could find on some earlier pass that nothing needs to be swapped. That is, all adjacent pairs are already in the correct order. In this case, there is no need to go on to subsequent passes, for the sort is complete already. If the list started in sorted order, this would happen on the very first pass. If it started in reverse order, it would not happen until the last one.
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular