What is Heap Sort

In heap sort the file to be sorted is interpreted as a binary tree. The sorting technique is implemented using array, which is a sequential representation of binary tree. The positioning of a node is given as follows

For a node at position i the parent is at position i/2, the left child is at position 2i and right child is at position 2i+1 ( 2i and 2i+1 <=n, otherwise children do not exist).

Heap sort is a two stage method. In the first stage the tree representing the input data is converted into a heap. A heap can be defined as a complete binary tree with the property that the value of each node is at least as large as the value of its children nodes. This, in turn, gives the root of the tree as the largest key. In the second stage the output sequence is generated in decreasing order by outputting the root and restructuring the remaining tree into a heap.

Example

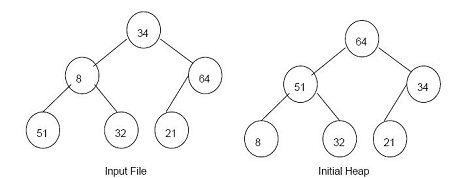
The list of numbers 34, 8, 64, 51, 32, 21 is arranged in an array initially as in Input file of the example given below. Here the value of n is 6, hence the least parent is 6/2 = 3. Left child of 64 (index 3) is compared with largest child, since 64 > 21 it is retained in its position. Parent 8 (index 2) is compared with its largest child 51 and are interchanged since 8 < 51. Now root 31(index 1) is compared with its largest child 64 and are interchanged since 34 < 64 and is shown in initial heap.

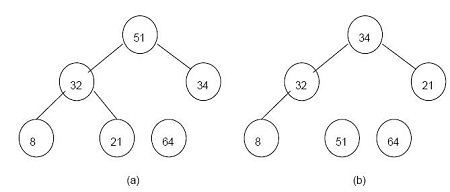
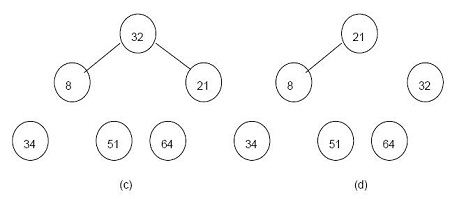
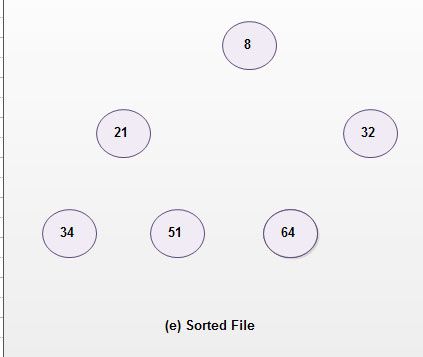
In fig (a) given below, the first largest number 64 which was brought into root is interchanged with the last element 21 (index 6) in the tree. For easy identification of arranged elements the edge is removed from its parent. In fig (b) given below, the same procedure is followed to bring 51 to root and is interchanged with the element in index 5. The same step is followed in fig (c) and fig (d) to get a sorted file as given in fig (e)

Algorithm 1 : Heap Sort implementation

Heap is an algorithm which sorts the given set of numbers using heap sort technique. Where ‘n’ is the number of elements, ‘a’ is the array representation of elements in the input binary tree. The heap algorithm 1 calls adjust algorithm 2 each time when heaping is needed.

heap(a,n)

{

Int i,t;

for(i=n/2;i>=1;i–)

{

adjust(a,i,n);

}

for(i=n;i>=2;i–)

{

t=a[i];

a[i]=a[1];

a[i]=t;

adjust(a,1,i-1);

}

}

Algorithm 2

adjust(int x[10],int i, int n)

{

int item, j;

j=2 * i;

item = x[i];

while (j <=n)

{

if((j<n)&&(x[j]<x[j+1]))

j=j+1;

if(item>=x[j])

break;

x[j/2]=x[j];

j=2 * j;

}

x[j/2]=item;

return 0;

}