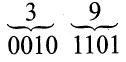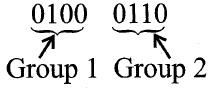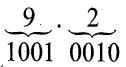Computer Notes

Header Right

Home » Electronics » Binary

Alphanumeric Codes

By Dinesh Thakur

Earlier computers were used only for the purpose of calculations i.e. they were only used as a calculating device. But now computers are not just used for numeric representations, they are also used to represent information such as names, addresses, item descriptions etc. Such information is represented using letters and symbols. Computer is a digital system and can only deal with l’s and 0’s. So to deal with letters and symbols they use alphanumeric codes.

Alphanumeric codes, also called character codes, are binary codes used to represent alphanumeric data. The codes write alphanumeric data, including letters of the alphabet, numbers, mathematical symbols and punctuation marks, in a form that is understandable and process able by a computer. Using these codes, we can interface input-output devices such as keyboards, monitors, printers etc. with computer.

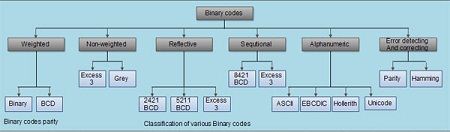
Several coding techniques have been invented that represent alphanumeric information as a series of l’s and O’s. The earliest better-known alphanumeric codes were the Morse code used in telegraph and 12-bit Hollerith code used when punch cards were used as a medium of inputting and outputting data. As the punched cards have completely vanished with the evolution of new mediums, the Hollerith code was rendered obsolete. Now the ASCII and EBCDIC codes are the two most widely used alphanumeric codes. The ASCII Code is very popular code used in all personal computers and workstations whereas the EBCDIC code is mainly alphanumeric code, the UNICODE, has evolved to overcome the limitation of limited character encoding as in case of ASCII and EBCDIC code.

Types of alphanumeric code.

MORSE CODE 

The Morse code, invented in 1837 by Samuel F.B. Morse, was the first alphanumeric code used in telecommunication. It uses a standardized sequence of short and long elements to represent letters, numerals and special characters of a given message. The short and long elements can be formed by sounds, marks, pulses, on off keying and are commonly known as dots and dashes. For example : The letter ‘A’ is formed by a dot followed by a dash. The digit 5 is formed by 5 dots in succession. The International Morse code treats a dash equal to three dots. To see the details of Morse code table you can refer the Internet search engines.

Due to variable length of Morse code characters, the morse code could not adapt to automated circuits. In most electronic communication, the Baudot code and ASCII code are used.

Morse code has limited applications. It is used in communication using telegraph lines, radio circuits. Pilots and air traffic controllers also use them to transmit their identity and other information.

BAUDOT CODE

The Baudot code was another popular alphanumeric code used in early 1860’s. It was invented by the French engineer Emile Baudot in 1870. It is a 5-unit code (i.e. it uses five elements to represent an alphabet). Moreover, unlike the Morse code, all the symbols all of equal duration. This allowed telegraph transmission of the Roman alphabet and punctuation and control signals.

HOLLERITH CODE

In 1896, Herman Hollerith formed a company called the Tabulating Machine Company. This company developed a line of machines that used punched cards for tabulation. After a number of mergers, this company was formed into the IBM, Inc. We often refer to the punched-cards used in computer systems as Hollerith cards and the 12-bit code used on a punched-card is called the Hollerith code.

A Hollerith string is a sequence of l2-bit characters; they are encoded as two ASCII characters, containing 6 bits each. The first character contains punches 12,0,2,4,6,8 and the second character contains punches 11, 1,3,5, 7, 9. Interleaving the two characters gives the original 12 bits. To make the characters printable on ASCII terminals, bit 7 is always set to 0 and bit 6 is said to the complement of bit 5. These two bits are ignored when reading Hollerith cards.

Today, as punched cards are mostly obsolete and replaced with other storage medias so the Hollerith code is rendered obsolete.

American Standard-Code for Information Interchange (ASCII)

The American Standard-Code for Information Interchange (ASCII) pronounced “as-kee” is a 7-bit code based on the ordering of the English alphabets. The ASCII codes are used to represent alphanumeric data in computer input/output.

Historically, ASCII developed from telegraphic codes. It was first published as a standard in 1967. It was subsequently updated and many versions of it were launched with the most recent update in 1986. Since it is a seven-bit code, it can almost represent 128 characters. These include 95 printable characters including 26 upper-case letters (A to Z), 26 lowercase letters (a to z), 10 numerals (0 to 9) and 33 special characters such as mathematical symbols, space character etc. It also defines codes for 33 non-printing obsolete characters except for carriage return and/or line feed. The below table lists the 7 bit ASCII code containing the 95 printable characters.

                       American Standard-Code for Information Interchange (ASCII) pronounced

 

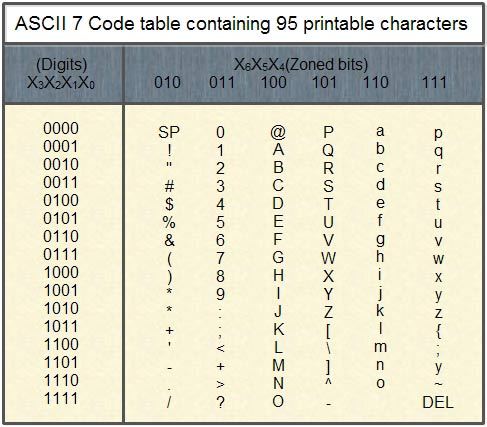
The format of ASCII code for each character is X6‘ ·Xs, X4, X3, X2, Xl‘ X0 where each X is 0’ or 1. For instance, letter D is coded as .1000100. For making reading easier, we leave space as follows: 1000100.

Similarly, from the above table, we see that letter ‘A’ has X6 X5X4 of 100 and X3 X2 Xl Xo of 0001 (A). Similarly, the digit ‘9’ has X6 X5 X4 values of 011 and X3 X2 Xl X0 of 1001 so the ASCII-7 code for digit 9 is 0111001.

More examples are:

The ASCll-7 code for ‘d’ is 1100100 as seen from the table 3.4.

The ASCll-7 code for ‘+’ is 0101011 as seen from the table 3.4.

An eight-bit version of the ASCII code, known as US ASCII-8 or ASCII-8, has also been developed. Since it uses 8-bits, so this version of ASCII can represent a maximum of 256 characters.

The table below lists some ASCII-8 codes.

When the ASCII -7 codes was introduced, many computers dealt with eight -bit groups (or bytes) as the smallest unit of information. This eight bit code was commonly used as parity bit for detection of error on communication lines. Machines that did not use the parity bit typically set the eighth bit to O. In that case, the ASCII code format would be X7 X6 X5 X4 X3 X2 Xl X0‘ In case of ASCII-7 code, if this representation is chosen to represent characters then X7 would always be zero. So, the eight-bit ASCII-7 code for ‘A’ would be 01000001 and for 4’ would be 00101011.

                        ASCII-8 codes

 

Example 1: With an ASCII-7 keyboard, each keystroke produces the ASCII equivalent of the designated character. Suppose that you type PRINT X. What is the output of an ASCII-7 keyboard?

Solution: The sequence is as follows:

The ASCII-7 equivalent of P = 101 0000

The ASCII-7 equivalent of R = 101 0010

The ASCII-7 equivalent of I = 1001010

The ASCII-7 equivalent of N = 100 1110

The ASCII-7 equivalent of T = 1-010100

The ASCII-7 equivalent of space = 010 0000

The ASCII-7 equivalent of X = 101 1000

So the output produced is 1010000101001010010101001110101010001000001011000. The output in hexadecimal equivalent is 50 52 49 4E 54 30 58

Example2: A computer sends a message to another computer using an odd-parity bit. Here is the message in ASCII-8 Code.

1011 0001

1011 0101

1010 0101

1010 0101

1010 1110

What do these numbers mean?

Solution

On translating, the 8-bit numbers into their equivalent ASCII-8 code we get the word 1011 0001 (Q), 10110101 (U), 10100101 (E), 1010 0101 (E), 1010 1110 (N)

So, on translation we get QUEEN as the output.

Extended Binary Coded Decimal Interchange Code (EBCDIC)

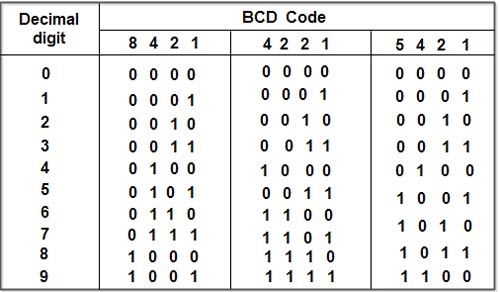
The Extended Binary Coded Decimal Interchange Code (EBCDIC) pronounced as “ebi-si disk” is another frequently used code by computers for transferring alphanumeric data. It is 8-bit code in which the numerals (0-9) are represented by the 8421 BCD code preceded by 1111. Since it is a 8-bit code, it can almost represent 23 (= 256) different characters which include both lowercase and uppercase letters in addition to various other symbols and commands.

                   EBCDIC CODE TABLE

 

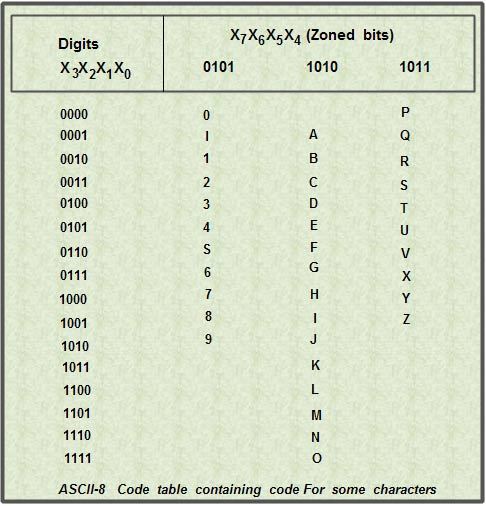
EBCDIC was designed by IBM corp. so it is basically used by several IBM· models. In this code, we do not use a straight binary sequence for representing characters, as was in the case of ASCII code. Since it is a 8-bit code, so it can be easily grouped into groups of 4 so as to represent in arm of hexadecimal digits. By using the hexadecimal number system notation, the amount of digits used to represent various characters and special characters using EBCDIC code is reduced in volume of one is to four. Thus 8-bit binary code could be reduced to 2 hexadecimal digits which are easier to decode if we want to view the internal representation in memory. The above table lists the EBCDIC code for certain characters.

Read the above table as you read the graph. Suppose you want to search for EBCDIC code for letter ‘A’. To that case, the value of X3 X2 Xl X0 bits is 0001 and value X7 X6 X5 X4 bits is 1100.

Therefore, EBCDIC code for letter ‘A’ is 11000001(A). Similarly, the EBCDIC code for ‘B’ is 11000010(B).

The EBCDIC code ‘=’ is 01111110

The EBCDIC code for ‘$’ is 0101 1011

UNICODE

The ASCII and EBCDIC encodings and their variants that we have studied suffer from some limitations.

1. These encodings do not have a sufficient number of characters to be able to encode alphanumeric data of all forms, scripts and languages. As a result, they do not permit multilingual computer processing.

2. These encoding suffer from incompatibility. For example: code 7A (in hex) represents the lowercase letter ‘Z’ in ASCII code and the semicolon sign ‘;’ in EBCDIC code.

To overcome these limitations, UNICODE also known as universal code was developed jointly by the Unicode Consortium and the International Organization for Standardization (ISO). The Unicode is a 16-bit code so it can represent 65536 different characters. It is the most complete character encoding scheme that allows text of all forms and languages to be encoded for use by computers. In addition to multilingual support, it also supports a comprehensive set of mathematical and technical symbols, greatly simplifying any scientific information interchange.

UNICODE has a number of uses

1. It is increasingly being used for internal processing and storage of text. Window NT and its descendents, Java environment, Mac OS all follow Unicode as the sole internal character encoding.

2. All World Wide Web consortium recommendations have used Unicode as their document character set since HTML 4.0.

3. It partially addresses the new line problem that occurs when trying to read a text file on different platforms. It defines a large number of characters that can be recognized as line terminators.

Unicode is currently being adopted by top computer industry leaders like Microsoft, Apple, Oracle, Sun, SAP and many more in their products.

 

Gray code

By Dinesh Thakur

The Gray code was designed by Frank Gray at Bell Labs in 1953. It belongs to a class of codes called the minimum change code. The successive coded characters never differ in more than one-bit. Owing to this feature, the maximum error that can creep into a system using the binary gray code to encode data is much less than the worst -case error encountered in case of straight binary encoding.

The Gray code is an unweighted code. Because of this, the· gray code is not suitable for arithmetic operations but finds applications in input/output devices, some analog-to-digital converters and designation of rows and columns in Karnaugh map etc.

The table below lists the gray code equivalents of the decimal number 0 – 15.

                      the gray code equivalents of the decimal number 0 - 15

 

                     gray codes

One can easily remember the gray codes. A three-bit gray code can be obtained by merely reflecting the two-bit code about an axis at the end of the code and assigning a third-bit as 0 above the axis and as 1 below the axis. The reflected gray code is nothing but code written in reverse order. By reflecting three-bit code, a four-bit code may be obtained.

                   gray codes

Now let us consider a few examples. The four-bit gray code for decimal number 39 is 00101101.

Similarly, gray code for (923.1)10 and (327) is

(923.1)10 = (1101 0011 0010.0001) Gray code

(327)10 = (100011 0100) Gray code

Excess-3 Code (XS3)

By Dinesh Thakur

Excess-3, also called XS3, is a non-weighted code used to express decimal number-s. It is another important binary code. It is particularly significant for arithmetic operations as it overcomes the shortcomings encountered while using the 8421 BCD code to add two decimal digits whose sum exceeds 9. This code is used in some old computers.

The Excess-3 code for a given decimal number is determined by adding ‘3’ to each decimal digit in the given number and then replacing each digit of the newly found decimal number by its four bit binary equivalent. The table gives is the Excess-3 code. For example, XS3 code of 24 is obtained as

  2       4

+3    +3

  5       7

0101 0111

Thus, XS3 code of 24 is 0101 0111.

The key feature of the Excess-3 code is .that it is self complementing. In other words, the l’s complement of an Excess- 3 number is the Excess- 3 code for the 9’s complement of the corresponding decimal number. For example, the Excess- 3 code for decimal 6 is 1001. The l’s complement of 1001 is 0110, which is the Excess-3 code for decimal 3, and 3 is the 9’s complement of 6. This property of Excess-3 code makes it useful in some arithmetic operations.

Now let us consider a few examples. The Excess-3 code for decimal number 27 is 01011010.

Similarly, Excess-3 code for (597)10 and (14.57)10 is

(597)10 = (100011001010)

(14.57)10 = (01000111.10001010)

One should note that corresponding to given Excess-3 code, the equivalent decimal number can be determined by first splitting the number into four-bit groups, starting from radix point and then subtracting 0011 from each four-bit group. This gives us 8421 BCD equivalent of the given Excess-3 code, which can then be converted into the equivalent decimal number. For example; Let us suppose we want to determine the decimal equivalent for the Excess-3 code 1000110. First we make group of 4 bits starting from radix point.

Subtracting 0011 from each group, we obtain the new number as 00010011. Its decimal equivalent is 13.

Therefore, (1000110) Excess-3= (13)10

 

BINARY CODED DECIMAL (BCD)

By Dinesh Thakur

The binary coded decimal (BCD) is a type of binary code used to represent a given decimal number in an equivalent binary form. Its main advantage is that it allows easy conversion to decimal digits for printing or display and faster calculations.

The most common BCD code is the 8421 BCD code. In this, the BCD equivalent of a decimal number is written by replacing each decimal digit in integer and fractional parts with its four-bit binary equivalent ‘(or nibble). Here 8, 4, 2 and 1 represent the weights of different bits in the four-bit groups, starting from the (MSB) most significant bit (to extreme left) and proceeding towards the least significant (LSB) bit.

This feature makes it a weighted code, whose main characteristic is that each binary digit in the four bit group representing a given decimal digit is assigned a weight, and for each group of four bits, the sum of the weights of those binary digits whose value is 1 is equal to the decimal digit which they represent.

For example, if we look at table, we find that the decimal digit 9 when represented in 8421 BCD is 1001. Now the decimal digit assigned to first 1 is 8 and to the second 1 is 1. If we add 8 and 1 we get the required decimal number which is 9.

 BCD Code Chart

The 4221 BCD and 5421 BCD are other weighted BCD codes shown in table. The numbers 4, 2, 2, 1 in 4221 BCD and 5, 4, 2 and 1 in 5421 BCD represent weights of the relevant bits.

Now let us consider some examples, where we convert the given decimal numbers to BCD.

The 8421 BCD code for 9.2 is 1001.0010.

 BCD for 9.2

The 4221 BCD code for 9.2 is 1111.0010.

The 5421 BCD code for 9.2 is 1100.0010.

BCD code is useful for outputting to displays that are always numeric (0 to 9), such as those found in digital clocks or digital voltmeters.

Classification of Various Binary Code

By Dinesh Thakur

Digital data is represented, stored and transmitted as groups of binary digits also known as binary code. The binary codes can be classified as shown in Fig.

Classification of various binary code

Weighted codes: In weighted codes, each digit is assigned a specific weight according to its position. For example, in 8421BCD code, 1001 the weights of 1, 0, 0, 1 (from left to right) are 8, 4, 2 and 1 respectively.

Suppose W1‘ W2‘ W3 and W4 are the weights of binary digits and Xl‘ X2, X3 and X4 are the corresponding digit values then decimal digit. N = W1 Xl + W2 X2 + W3 X3 + W4 X4 is represented by binary sequence X4 X3 X2 X4.

The codes 8421BCD, 2421BCD, 5211BCD are all weighted codes.

• Non-weighted codes: The non-weighted codes are not positionally weighted. In other words, each digit position within the number is not assigned a fixed value ( or weight ).

             Excess-3 and gray code are non-weighted codes.

• Reflective codes: A code is reflective when the code is self complementing. In other words, when the code for 9 is the complement the code for 0, 8 for 1, 7 for 2, 6 for 3 and 5 for 4.

             2421BCD, 5421BCD and Excess-3 code are reflective codes.

• Sequential codes: In sequential codes, each succeeding ‘code is one binary number greater than its preceding code. This property helps in manipulation of data.

             8421 BCD and Excess-3 are sequential codes.

• Alphanumeric codes: Codes used to represent numbers, alphabetic characters, symbols and various instructions necessary for conveying intelligible information.

             ASCII, EBCDIC, UNICODE are the most-commonly used alphanumeric codes.

• Error defecting and correcting codes: Codes which allow error defection and correction are called error detecting and’ correcting codes. Hamming code is the mostly commonly used error detecting and correcting code.