In this Armstrong Number in python tutorial, we will write a python program for Armstrong’s number (also called narcissistic number). Before we proceed throughout the program, let’s see what’s an Armstrong number, after which we’ll check whether a predetermined number is Armstrong number or not. So within this tutorial, we will discuss more Armstrong numbers in Python and code a program in Python.
We’ll be covering the following topics in this tutorial:
What is an Armstrong Number?
Definition: An Armstrong number or Narcissistic number is an n-digit number equivalent to the sum of digits raised to the nth power of digits from the number. A few Armstrong numbers are: 0, 1, 2, 3, 153, 370, 407, 1634, 8208, etc.
Armstrong’s number is a particular type of number, where every digit is raised to the power of the number of digits and ultimately summed of digits to get a number. If the number thus discovered is the same as the number initially accepted, then the respective number is called an Armstrong number. A good illustration of Armstrong’s number is 407. As soon as we break down the digits of 407, they’re 4, 0, and 7. Then we find every digit raised to the power of the number of digits, and at last, we calculate the sum of those numbers.
Armstrong Number Logic
abcd... = pow(a,n) + pow(b,n) + pow(c,n) + pow(d,n) + ....
where n denotes the number of digits in the number
Let’s try to understand why 407 is an Armstrong number.
Let’s example it using mathematical computation.
Example: 407 407 = (4)3 + (0)3 + (7)3 = 64 + 0 + 343 = 407
Algorithm to check given number is Armstrong number or not
START Step 1 → Initialize result = 0 and temp = number. Step 2 → Find the total number of digits in the number. Step 3 → Repeat until (temp != 0) Step 4 → remainder = temp % 10 Step 5 → result = result + pow(remainder,n) Step 6 → temp = temp / 10 Step 7 → if (result == number) Step 8 → Print Armstrong Number Step 9 → Else Step 10 → Print Not an Armstrong Number STOP
Pseudocode for Armstrong number
Below is the procedure for Armstrong number in C
temp = num rem = 0 WHILE temp IS NOT 0 rem ← temp modulo 10 sum ← sum + power(rem, digits); divide temp by 10 END WHILE IF sum equivalent to num PRINT Armstrong Number ELSE PRINT not an Armstrong Number END IF end procedure
Python program for Armstrong number
You can check whether a given number is Armstrong number or not in Python in number of ways:
num = int(input("Please enter a number: "))
str_num = str(num)
len_num = len(str_num)
digits_sum = 0
for d in str_num:
digits_sum += int(d) ** len_num # power operation
if num == digits_sum:
print("{} is an Armstrong number of order {}".format(num,len_num))
else:
print("{} is NOT an Armstrong number".format(num))
Output:
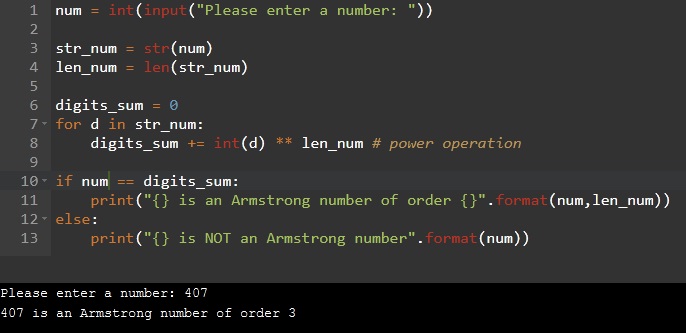 Following are the steps in the above program
Following are the steps in the above program
• We accept input from consumers and convert them to Some numbers.
• We convert the number to a string and find its length.
• Then we iterate through each digit and find the sum of these digits raised to the string’s power of length.
• Ultimately, we check whether the sum precisely likes as the first number. If they’re the same, this number is an Armstrong number.
Python Program using math module
#Python program to check whether the given number is Armstrong or not
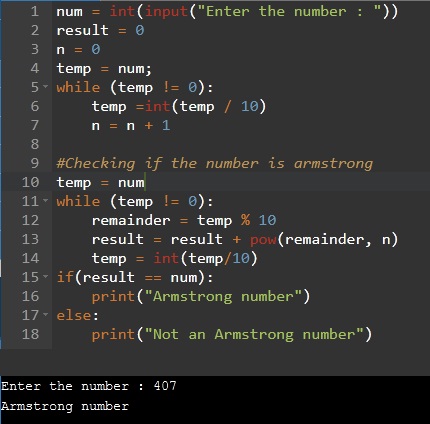
num = int(input("Enter the number : "))
result = 0
n = 0
temp = num;
while (temp != 0):
temp =int(temp / 10)
n = n + 1
#Checking if the number is armstrong
temp = num
while (temp != 0):
remainder = temp % 10
result = result + pow(remainder, n)
temp = int(temp/10)
if(result == num):
print("Armstrong number")
else:
print("Not an Armstrong number")
Output:
Python Program using a while loop
#program to check whether the given number is Armstrong or not using a while loop
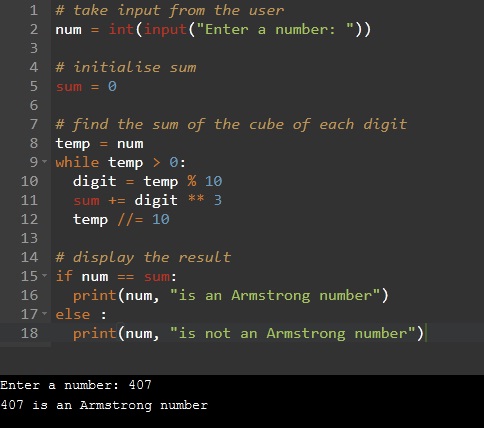
# take input from the user
num = int(input("Enter a number: "))
# initialise sum
sum = 0
# find the sum of the cube of each digit
temp = num
while temp > 0:
digit = temp % 10
sum += digit ** 3
temp //= 10
# display the result
if num == sum:
print(num, "is an Armstrong number")
else :
print(num, "is not an Armstrong number")
Output:
 Program Explanation
Program Explanation
We take input from the consumer and check that the entered number is the Armstrong number. We initialize sum = 0 and receive each digit number using the ‘%(modulo)’ operator. When that number is divided by 10, then the rest is the last digit of this number. The cubes of these digits are assessed by utilizing the ‘exponent(*)’ operator. Using the ‘if-else’ condition, we compare the sum with the original number. If they’re equivalent, then we affirm it is an Armstrong number.
While Loop makes certain the specified number is greater than 0, statements within the while loop divide the numbers and count the number of individual digits within the set number.
while Temp > 0: Times = Times + 1 Temp = Temp // 10
The Python Second While loop makes sure that the specified number is greater than 0.
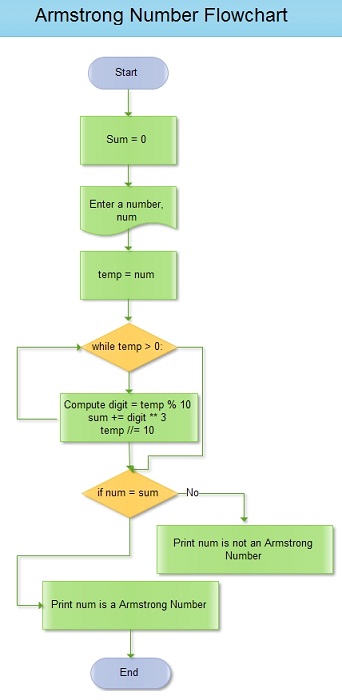
Armstrong Numbers Flowchart
 Python program to print Armstrong numbers within the given range in Python
Python program to print Armstrong numbers within the given range in Python
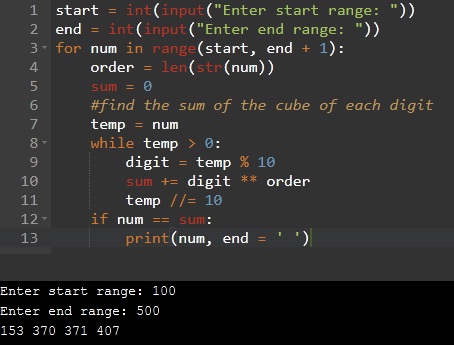
#program to print Armstrong numbers within the given range in Python
start = int(input("Enter start range: "))
end = int(input("Enter end range: "))
for num in range(start, end + 1):
order = len(str(num))
sum = 0
#find the sum of the cube of each digit
temp = num
while temp > 0:
digit = temp % 10
sum += digit ** order
temp //= 10
if num == sum:
print(num, end = ' ')
Output:
 Let us see the working principle of this while loop in iteration wise
Let us see the working principle of this while loop in iteration wise
How it works:
This table Shows Exactly What Occurs at each iteration of the while loop (assuming the num = 407):
| Iteration | rem | sum | num |
| After 1st iteration | rem = 407%10 = 7 | sum = 0 + (4)3 = 64 | num = 407 / 10 = 40 |
| After 2st iteration | rem = 40%10 = 0 | sum = 64 + (0)3 = 64 | num = 40 / 10 = 4 |
| After 3st iteration | rem = 4%10 = 4 | sum = 64 + (7)3 = 343 | num = 4 / 10 = 0 |
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular