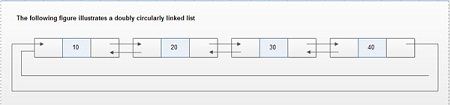
In a doubly-circularly-linked list, each node has two links, similar to a doubly-linked list, except that the previous link of the first node points to the last node and the next link of the last node points to the first node. As in doubly-linked lists, insertions and removals can be done at any point with access to any nearby node.
Circularly linked lists are useful to traverse an entire list starting at any point. In a linear linked list, it is required to know the head pointer to traverse the entire list. The linear linked list cannot be traversed completely with the help of an intermediate pointer.
Access to any element in a doubly circularly linked list is much easier than in a linearly linked list since the particular element can be approached in two directions. For example to access an element present in the fourth node of a circularly linked list having five elements, it is enough to start from the last node and traverse the list in the reverse direction to get the value in the fourth node.
Implementation of a circular linked list:
Creating the list
while (input_element != -999)
{
new_node=(struct node *) malloc (size);
new_node->info=input_element;
if ( root_node==NULL )
root_node=new_node;
else
( *last_node )->next=new_node;
(*last_node)=new_node;
scanf(“%d”,&input_element);
}
if(root!=NULL)
new->next=root;
return root;
Inserting elements into the list
After getting the position and value to be inserted, the following code can be followed:
new_node=(struct node *)malloc(sizeof(struct node));
new_node-> info=input_element;
if((position==1)||((*root_node)==NULL))
{
new_node->next =*root_node;
*root_node = new_node;
if((*last_node)!=NULL)
(*last_node)->next=*root_node;
else
*last_node=*start_node;
}
else
{
temp_node=*root_node;
counter=2;
while ( (counter<position) && (temp_node->next !=
(*root_node) ) )
{
temp_node=temp_node->next;
++counter;
}
if(temp_node->next==(*root_node))
*last_node=new_node;
new_node->next=temp_node->next;
temp_node->next=new_node;
}
Deleting an element from the list
After getting the element to be deleted, the following code can be used:
If(*front_node != NULL)
{
printf(“The item deleted is %d”,(*front_node->info));
If (*front_node == *rear_node)
{
*front_node = *rear_node = NULL;
}
else
{
*front_node = *front_node->next;
*rear_node->link = *front_node;
}
}
Processing a graph requires the ability to traverse the graph. Traversing a graph is similar to traversing a binary tree, except that traversing a graph is a bit more complicated. Recall that a binary tree has no cycles. Also, starting at the root node, we can traverse the entire tree.
On the other hand, a graph might have cycles and we might not be able to traverse the entire graph from a single vertex (for example, if the graph is not connected). Therefore, we must keep track of the vertices that have been visited. We must also traverse the graph from each vertex (that has not been visited) of the graph.
This ensures that the entire graph is traversed. The two most common graph traversal algorithms are the depth first traversal and breadth first traversal, which are described next. For simplicity, we assume that when a vertex is visited, its index is output. Moreover, each vertex is visited only once. We use the bool array visited to keep track of the visited vertices.
The depth first traversal is similar to the preorder traversal of a binary tree. An initial or source vertex is identified to start traversing, then from that vertex any one vertex which is adjacent to the current vertex is traversed i.e. only one adjacent vertex is traversed from the vertex which had been traversed last.
The general algorithm is:
for each vertex v in the graph
if v is not visited
start the depth first traversal at v
The general algorithm to do a depth first traversal at a given node v is:
1. Mark node v as visited
2. Visit the node
3. For each vertex u adjacent to v
a. if u is not visited
b. start the depth first traversal at u
c. Clearly, this is a recursive algorithm.
The breadth first traversal of a graph is similar to traversing a binary tree level by level (the nodes at each level are visited from left to right).All the nodes at any level, i, are visited before visiting the nodes at level i + 1.
As in the case of the depth first traversal, because it might not be possible to traverse the entire graph from a single vertex, the breadth first traversal also traverses the graph from each vertex that is not visited. Starting at the first vertex, the graph is traversed as much as possible; we then go to the next vertex that has not been visited. In other words it can be stated as all vertices that are adjacent to the current vertex are traversed first. To implement the breadth first search algorithm, we use a queue.
The general algorithm is:
a.for each vertex v in the graph
if v is not visited
add v to the queue // start the breadth first search at v
b. Mark v as visited
c. while the queue is not empty
c.1. Remove vertex u from the queue
c.2. Retrieve the vertices adjacent to u
c.3. for each vertex w that is adjacent to u
if w is not visited
c.3.1. Add w to the queue
c.3.2. Mark w as visited
Example The Depth first search for the above undirected graph
A, B, E, C, D
The Depth first search for the above undirected graph
A, B, C, D, E
Shortest path can be calculated only for the weighted graphs. The edges connecting two vertices can be assigned a nonnegative real number, called the weight of the edge. A graph with such weighted edges is called a weighted graph.
Let G be a weighted graph. Let u and v be two vertices in G, and let P be a path in G from u to v. The weight of the path P is the sum of the weights of all the edges on the path P, which is also called the weight of v from u via P.
Let G be a weighted graph representing a highway structure. Suppose that the weight of an edge represents the travel time. For example, to plan monthly business trips, a salesperson wants to find the shortest path (that is, the path with the smallest weight) from her or his city to every other city in the graph. Many such problems exist in which we want to find the shortest path from a given vertex, called the source, to every other vertex in the graph. This section describes the shortest path algorithm, also called the greedy algorithm, developed by Dijkstra.
Shortest Path
Given a vertex, say vertex (that is, a source), this section describes the shortest path algorithm.
The general algorithm is:
1. Initialize the array smallestWeight so that smallestWeight[u] = weights[vertex, u].
2. Set smallestWeight[vertex] = 0.
3. Find the vertex, v, that is closest to vertex for which the shortest path has not been determined.
4. Mark v as the (next) vertex for which the smallest weight is found.
5. For each vertex w in G, such that the shortest path from vertex to w has not been determined and an edge (v, w) exists, if the weight of the path to w via v is smaller than its current weight, update the weight of w to the weight of v + the weight of the edge (v, w).
Because there are n vertices, repeat Steps 3 through 5, n – 1 times.
Example : Shortest Path
Both the malloc() and the calloc() functions are used to allocate dynamic memory. Each operates slightly different from the other. malloc() takes a size and returns a pointer to a chunk of memory at least that big:
void *malloc( size_t size );
calloc() takes a number of elements, and the size of each, and returns a pointer to a chunk of memory at least big enough to hold them all:
void *calloc( size_t numElements, size_t sizeOfElement );
There’s one major difference and one minor difference between the two functions. The major difference is that malloc() doesn’t initialize the allocated memory. The first time malloc() gives you a particular chunk of memory, the memory might be full of zeros. If memory has been allocated, freed, and reallocated, it probably has whatever junk was left in it. That means, unfortunately, that a program might run in simple cases (when memory is never reallocated) but break when used harder (and when memory is reused). calloc() fills the allocated memory with all zero bits. That means that anything there you’re going to use as a char or an int of any length, signed or unsigned, is guaranteed to be zero. Anything you’re going to use as a pointer is set to all zero bits. That’s usually a null pointer, but it’s not guaranteed.Anything you’re going to use as a float or double is set to all zero bits; that’s a floating-point zero on some types of machines, but not on all.
The minor difference between the two is that calloc() returns an array of objects; malloc() returns one object. Some people use calloc() to make clear that they want an array.
The free subroutine frees a block of memory previously allocated by the malloc subroutine. Undefined results occur if the Pointer parameter is not a valid pointer. If the Pointer parameter is a null value, no action will occur.
The realloc () function is used to allocate memory and has the following prototype:
void * realloc (void * ptr, unsigned int num);
The function modifies the size of the previously allocated memory pointed to by *ptr to that specified by a. The value of a may be higher or lower than the original. A pointer to the block is returned because realloc () may need to move the block to increase its size. If this occurs, the old block content is copied into the new block, and no information is lost. If ptr is null, allocates size bytes and returns a pointer; if size is zero, the memory pointed to by ptr is released. If there is not enough memory to allocate, a null pointer is returned and the original block is left unchanged.
To avoid waste of memory or the memory leak (memory leaks), then we should do the reallocation of the spaces memory previously allocated by function malloc (), calloc () or realloc (). In the C language, this process will be carried out by using function free () which has the form of a pointer parameter. Here is the prototype of function free ().
void *free(void *p);
p must be a pointer here previously allocated using function malloc (), calloc () or realloc (). Here is an example of use function free ().
The use of pointers will usually cause memory leaks, the event where there is room memory is wasted in vain because the memory space can no longer in access to allocated. This memory leak can result in programs or our operating system be damaged or have a hang. Here is an example of the syntax which will result in a memory leak.
#include <stdio.h>
#include<conio.h>
int main (void)
{
/* Declare a pointer P which would point to the type of data int */
void *P;
int x = 10;
double y = 15.3;
clrscr();
/* Ordered memory space to put the type int */
P = (int *) malloc (sizeof (int));
/* Ordered pointer P to point to the address of variable x */
P = & x;
/* Display the value contained in the pointer P */
printf ("The value of P \t =% p \n", P);
printf ("Value *P \t =% d \n \n", * ((int *) P));
/* Ordered memory space to put the type double */
P = (double *) malloc (sizeof (double));
/* Ordered pointer P to point to the address of variable y */
P = & y;
/* Display the value contained in the pointer P */
printf ("The value of P \t =% p \n", P);
printf ("Value *P \t =% .1f \n", * ((double *) P));
return 0;
}
At first glancethe above programasproperlyandifimplementedwouldalsoprovide the following result.
In the above program, initially we booked a space (memory address) to placing a value of type int (ie the address FFF2) then record it into a pointer P. After the process of the pointer, in we booked a room on back to hold the value of type double (ie FFEA address) and record it back to the pointer P. This resulted in pointer P who was appointed address FFF2 move to point to FFEA address, so the address is no longer accessible FFF2 will result in the waste of memory space is wasted. This kind of incident called with a memory leak.
To avoid this, we should free FFF2 address before ordering pointer P to point to the new address, namely by using the function free (). Thus, the syntax of the program should write as follows.
#include <stdio.h>
#include<conio.h>
int main (void)
{
void * P;
int x = 10;
double y = 15.3;
clrscr();
P = (int *) malloc (sizeof (int));
P = & x;
printf ("The value of P \t =% p \n", P);
printf ("Value *P \t =% d \n \n", * ((int *) P));
/* Free pointer P with the function free () */
free (P);
P = (double *) malloc (sizeof (double));
P = & y;
printf ("The value of P \t =% p \n", P);
printf ("Value *P \t =% .1f \n", * ((double *) P));
return 0;
}
malloc allocates memory for object in heap but doesn’t invoke object’s constructor to initiallize the object. new allocates memory and also invokes constructor to initialize the object. malloc() and free() do not support object semantics.
Does not construct and destruct objects string * ptr = (string *)(malloc (sizeof(string))) Are not safe Does not calculate the size of the objects that it construct Returns a pointer to void int *p = (int *) (malloc(sizeof(int))); int *p = new int; Are not extensible new and delete can be overloaded in a class “delete” first calls the object’s termination routine (i.e. its destructor) and then releases the space the object occupied on the heap memory. If an array of objects was created using new, then delete must be told that it is dealing with an array by preceding the name with an empty []:-
Int_t *my_ints = new Int_t[10];
…
delete []my_ints;
The function realloc () is used to resize the memory allocated earlier by function malloc () to a new size given by the second parameter of the function. The function realloc(ptr,n) uses two arguments.the first argument ptr is a pointer to a block of memory for which the size is to be altered. The second argument n specifies the new size. The size may be increased or decreased.
If n is greater than the old size and if sufficient space is not available subsequent to the old region, the function realloc( ) may create a new region and all the old data are moved to the new region.
Illustrates malloc() and realloc ().
#include <stdio.h>
#include<stdlib.h>
int main ()
{
int a= 0, n, m, i, j,k =0;
int* Array;
clrscr();
printf("Enter the number of elements of Array.");
scanf("%d", &n );
Array= (int*) malloc( n* sizeof(int) );
if( Array== NULL)
{
printf("Error. Out of memory.\n");
exit(0);
}
printf("Enter the %d elements of Array:", n);
for ( i =0; i<n; i++)
scanf("%d",&Array[i]);
for( j =0;j<n; j++)
printf("Array[%d] = %d\n", j, *(Array+j));
printf("Enter the number of elements of extended array.");
scanf("%d", &m);
Array= realloc(Array, m);
if( Array== NULL)
{
printf("realloc has failed.\n");
exit(0);
}
printf("Enter values of %d additional elements of array.", m-n);
for (k= n ; k<m; k++)
scanf("%d", &Array[k]);
for( a =0;a<m; a++)
printf("Array[%d] = %d\n", a, *(Array+ a));
return 0;
}
The malloc () function is used to allocate memory and has the following prototype:
void * malloc (unsigned int num);
malloc(…) takes in only a single argument which is the memory required in bytes. The function gets the number of bytes that we allocate (a) allocates memory and returns a pointer void * allocated to the first byte. The void * pointer can be assigned to any type of pointer. If there is not enough memory to allocate the requested memory malloc () returns a null pointer. malloc(…) allocated bytes of memory and not blocks of memory like calloc(…). See an example of dynamic allocation with malloc ():
#include <stdio.h>
#include <stdlib.h> /* To use malloc () */
main (void)
{
int *p;
int a;
int i;
... /* Determines the value to somewhere */
p = (int *) malloc (a * sizeof (int)); /* Allocate the integers p can now be treated as a vector the positions */
if (!p)
{
printf ("** Error: Insufficient Memory **");
exit;
}
for (i = 0; i<a; i ++) /* p can be treated as a vector with the positions */
p[i] = i * i;
...
return 0;
}
In the example above, is to allocate enough memory to store the integers. The sizeof () operator returns the number of bytes of an integer. It is useful to know the size of type. The pointer void * malloc () returns is converted to an int * and the cast is assigned to p. The following statement tests whether the operation was successful. If not, p has a null value, which will cause !P returns true. If the operation is successful, we can use the whole allocated vector normally, for example by indexing the p [0] a p [(a-1)].
The calloc () function also serves to allocate memory, but has a prototype a little different:
void * calloc (unsigned int a, unsigned int size);
The function allocates an amount of memory equal to a * size, that is, allocates enough memory to a vector of a size objects. Returns a void * pointer to the first byte allocated. The void * pointer can be assigned to any type of pointer. If there is not enough memory to allocate memory required to calloc () function returns a null pointer. By default the block is initialized to 0. The total number of memory allocated will be (number_of_elements * size). See an example of dynamic allocation with calloc ():
#include <stdio.h>
#include <stdlib.h> /* To use calloc () */
main (void)
{
int *p;
int a;
int i;
... /* Determines the value to somewhere */
p = (int *) calloc (a, sizeof (int)); /* Allocate the integers p can now be treated as a vector the positions */
if (!p)
{
printf ("** Error: Insufficient Memory **");
exit;
}
for (i = 0; i <a; i ++) / * p can be treated as a vector with the positions * /
p [i] = i * i;
...
return 0;
}
In the above example, memory is allocated enough to put the integers. The sizeof () operator returns the number of bytes of an integer. It is useful to know the size of type. The void * pointer that calloc () returns is converted to an int * and the cast is assigned to p. The following statement tests whether the operation was successful. If not, p has a null value, which will cause! P returns true. If the operation is successful, we can use the whole allocated vector normally, for example by indexing the p [0] ap [(a-1)].
1.) “new and delete” are preprocessors while “malloc() and free()” are functions. we dont use brackets will calling new or delete.
2.) No need of allocate the memory while using “new” but in “malloc()” we have to use “sizeof()”.
3.) “new” will initlize the new memory to 0 but “malloc()” gives random value in the new alloted memory location [better to use calloc()]
new() allocates continous space for the object instace
malloc() allocates distributed space.
new() is castless, meaning that allocates memory for this specific type,
malloc(), calloc() allocate space for void * that is cated to the specific class type pointer.
Record and record structures : The ::struct::record package provides a mechanism to group variables together as one data structure, similar to a ‘C’ structure. The members of a record can be variables or other records. However, a record can not contain circular record, i.e. records that contain the same record as a member.
This package was structured so that it is very similar to how Tk objects work. Each record definition creates a record object that encompasses that definition. Subsequently, that record object can create instances of that record. These instances can then be manipulated with the cget and configure methods.
The package only contains one top level command, but several sub commands (see below). It also obeys the namespace in which the record was define, hence the objects returned are fully qualified.
record define recordName recordMembers ? instanceName1
instanceName2 … ?
Defines a record. recordName is the name of the record, and is also used as an object command. This object command is used to create instances of the record definition. recordMembers are the members of the record that make up the record definition. These are variables and other record. If optional instanceName args are given, then an instance is generated after the definition is created for each instanceName.
record show record
Returns a list of records that have been defined.
record show instances recordName
Returns the instances that have been instantiated by recordName.
record show members recordName
Returns the members that are defined for record recordName. It returns the same
format as how the records were defined.
record show values instanceName
Returns a list of values that are set for the instance instanceName. The output is a list of key/value pairs. If there are nested records, then the values of the nested records will itself be a list.
record exists record recordName
Tests for the existence of a record with the name recordName.
record exists instance instanceName
Tests for the existence of a instance with the name instanceName.
record delete record recordName
Deletes recordName, and all instances of recordName. It will return an error if the
record does not exist.
record delete instance instanceName
Deletes instance with the name of instanceName. It will return an error if the
instance does not exist.
Record Members : Record members can either be variables, or other records, However, the same record can not be nested witin itself (circular). To define a nested record, you need to specify the record keyword, along the with name of the record, and the name of the instance of that nested record. For example, it would look like this :
# this is the nested record
record define mynestedrecord {
nest1
nest2
}
# This is the main record
record define myrecord {
mem1
mem2
{record mynestedrecord mem3}
}
Consider the following three examples. What do they all have in common?
Chocolate Cream Pie :
(1) Heat milk, marshmallows and chocolate in 3-quart saucepan over low heat, stirring constantly, until chocolate and marshmallows are melted and blended. Refrigerate about 20 minutes, stirring occasionally until mixture mounds slightly when dropped from a spoon.
(2) Beat whipping cream in chilled small bowl with electric mixer on high speed until soft peaks form. Fold chocolate mixture into whipped cream. Pour into pie shell. Refrigerate uncovered about 8 hours or until set. Garnish with milk chocolate curls and whipped cream.
How to change your motor oil
(1) Place the oil pan underneath the oil plug of your car.
(2) Unscrew the oil plug.
(3) Drain oil.
(4) Replace the oil plug.
(5) Remove the oil cap from the engine.
(6) Pour in 4 quarts of oil.
(7) Replace the oil cap.
Each of these examples is algorithm, a set of instructions for solving a problem. Once we have created an algorithm, we no longer need to think about the principles on which the algorithm is based. This means that algorithms are a way of capturing intelligence and sharing it with others. Once you have encoded the necessary intelligence to solve a problem in an algorithm, many people can use your algorithm without needing to become experts in a particular field.
Algorithms are especially important to computers because computers are really general purpose machines for solving problems. But in order for a computer to be useful, we must give it a problem to solve and a technique for solving the problem. Through the use of algorithms, we can make computers “intelligent” by programming them with various algorithms to solve problems. Because of their speed and accuracy, computers are well-suited for solving tedious problems such as searching for a name in a large telephone directory or adding a long column of numbers.
However, the usefulness of computers as problem solving machines is limited because the solutions to some problems cannot be stated in an algorithm.
Much of the study of computer science is dedicated to discovering efficient algorithms and representing them so that they can be understood by computers.
During our study of algorithms, we will discuss what defines an algorithm, how to represent algorithms, and what makes algorithms efficient. Along the way we will illustrate these concepts by introducing several algorithms for sorting. By the end of our study, you should be able to do the following:
1 Write some simple algorithms,
2 Sort numbers using three basic sorting algorithms, and
3 Compare the sorting algorithms for efficiency.
In the introduction, we gave an informal definition of an algorithm as “a set of instructions for solving a problem” and we illustrated this definition with a recipe, and instructions for changing the oil in a car engine. You also created your own algorithm for putting letters and numbers in order. While these simple algorithms are fine for us, they are much too ambiguous for a computer.
In order for an algorithm to be applicable to a computer, it must have certain characteristics. We will specify these characteristics in our formal definition of an algorithm.
An algorithm is a well-ordered collection of unambiguous and effectively computable operations that when executed produces a result and halts in a finite
amount of time [Schneider and Gersting 1995]. With this definition, we can identify five important characteristics of algorithms :
(1) Algorithms are well-ordered.
(2) Algorithms have unambiguous operations.
(3) Algorithms have effectively computable operations.
(4) Algorithms produce a result.
(5) Algorithms halt in a finite amount of time.
When writing algorithms, we have several choices of how we will specify the operations in our algorithm. One option is to write the algorithm using plain English. Although plain English may seem like a good way to write an algorithm, it has some problems that make it a poor choice. First, plain English is too wordy.
When we write in plain English, we must include many words that contribute to correct grammar or style but do nothing to help communicate the algorithm. Second, plain English is too ambiguous. Often an English sentence can be interpreted in many different ways. Remember that our definition of an algorithm requires that each operation be unambiguous.
Another option for writing algorithms is using programming languages. These languages are collections of primitives (basic operations) that a computer understands. While programming languages avoid the problems of being wordy
and ambiguous, they have some other disadvantages that make them undesirable for writing algorithms. Consider the following lines of code from the programming language C++.
a = 1;
b = 0;
while (a <= 10)
{
b = b + a;
a++;
}
cout << b;
This algorithm sums the numbers from 1 to 10 and displays the answer on the computer screen. However, without some special knowledge of the C++ programming language, it would be difficult for you to know what this algorithm does. Using a programming language to specify algorithms means learning special syntax and symbols that are not part of Standard English.
For example, in the code above, it is not very obvious what the symbol “++” or the symbol “<<” does. When we write algorithms, we would rather not worry about the details of a particular programming language. What we would really like to do is combine the familiarity of plain English with the structure and order of programming languages.
A good compromise is structured English. This approach uses English to write operations, but groups operations by indenting and numbering lines. An example of this approach is the directions for changing motor oil in the introduction lesson. Each operation in the algorithm is written on a separate line so they are easily distinguished from each other. We can easily see the advantage of this organization by comparing the structured English algorithm with the plain English algorithm.
For the remainder of this study, we will write our algorithms using the structured English approach.
Analysis of Algorithms (AofA) is a field in computer science whose overall goal is an understanding of the complexity of algorithms. While an extremely large amount of research is devoted to worst-case evaluations, the focus in these pages is methods for average-case and probabilistic analysis. Properties of random strings, permutations, trees, and graphs are thus essential ingredients in the analysis of algorithms.
To analyze an algorithm is to determine the amount of resources (such as time and storage) necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length. Usually the efficiency or complexity of an algorithm is stated as a function relating the input length to the number of steps (time complexity) or storage locations (space complexity).
Algorithm analysis is an important part of a broader computational complexity theory, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search of efficient algorithms.
Following steps must be followed to plan any algorithm :
(1) Device Algorithm : Creating an algorithm is an art in which may never be fully automated. When we get the problem, we should first analyse the given problem clearly and then write down some steps on the paper.
(2) Validate Algorithm : Once an algorithm is devised , it is necessary to show that it computes the correct answer for all possible legal inputs . This process is known as algorithm validation. The algorithm need not as yet be expressed as a program. It is sufficient to state it in any precise way. The purpose of validation is to assure us that this algorithm will work correctly independently of the issues concerning the programming language it will eventually be written in. Once the validity of the method has been shown, a program can be written and a second phase begins. This phase is referred to as program proving or program verification.
(3) Analyse Algorithm : As an algorithm is executed , it uses the computers central processing unit to perform operations and its memory ( both immediate and auxiliary) to hold the program and data. Analysis of algorithm or performance analysis refers to the task of determining how much computing time and storage an algorithm requires. An important result of this study is that it allows you to make quantitative judgments about the value of one algorithm over another. Another result is that it allows you to predict whether the software will meet any efficiency constraints that exist. Analysis can be made by taking into consideration.
(4) Test A Program : Testing a program consists of 2 phases : debugging and performance management. Debugging is the process of executing programs on sample data sets to determine whether results are incorrect if so corrects them. Performance management is the process of executing a correct program on data sets and measuring the time and space it takes to compute the results. These timing figures are useful in that they may confirm a previously done analysis and point out logical places to perform useful optimization.
A data structure is a way of organizing data that considers not only the items stored, but also their relationship to each other. Advance knowledge about the relationship between data items allows designing of efficient algorithms for the manipulation of data.
Compiler Design, Operating System, Database Management System, Statistical analysis package, Numerical Analysis, Graphics, Artificial Intelligence, Simulation
The heap is where malloc(), calloc(), and realloc() get memory. Getting memory from the heap is much slower than getting it from the stack. On the other hand, the heap is much more flexible than the stack. Memory can be allocated at any time and deallocated in any order. Such memory isn’t deallocated automatically; you have to call free().
Recursive data structures are almost always implemented with memory from the heap. Strings often come from there too, especially strings that could be very long at runtime. If you can keep data in a local variable (and allocate it from the stack), your code will run faster than if you put the data on the heap. Sometimes you can use a better algorithm if you use the heap faster, or more robust, or more flexible. Its a tradeoff.
If memory is allocated from the heap, its available until the program ends. That’s great if you remember to deallocate it when you’re done. If you forget, it’s a problem. A ?memory leak is some allocated memory that’s no longer needed but isn’t deallocated. If you have a memory leak inside a loop, you can use up all the memory on the heap and not be able to get any more. (When that happens, the allocation functions return a null pointer.) In some environments, if a program doesn’t deallocate everything it allocated, memory stays unavailable even after the program ends.