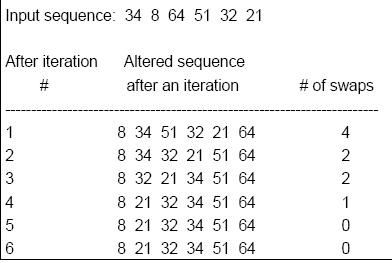
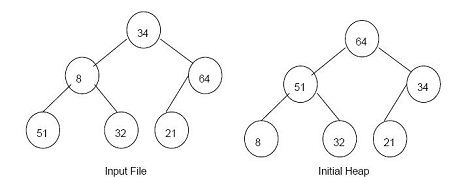
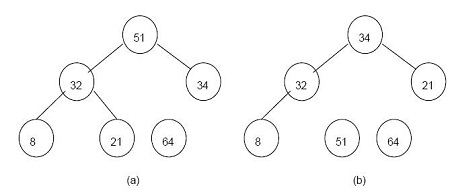
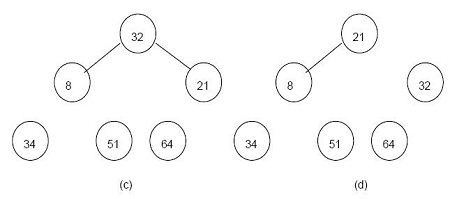
A class of algorithm that helps to provide very rapid access to data items that can be distinguished by some KEY value, for example a person’s name, or a filename. This key value is passed through a HASH FUNCTION which creates from it a number that is used as an index into a HASH TABLE containing pointers to the actual data items.
A simple hash function might be the alphabetic order of the first letter of a person’s name, so that, say, Pountain would hash to the 16th slot in the table. However, this would be a very poor hash function since every name beginning with P would hash to the same slot, an occurrence known as a hash clash or hash collision. Whenever such a collision occurs, the new item that caused it must be stored either in the next free adjacent table slot, or on a LIN KED LIST pointed to by the table slot. If too many such collisions occur, the algorithm degenerates into a case of LINEAR SEARCH. Designing a good hashing algorithm involves choosing a hash function that distributes the items widely and evenly, without requiring too large a hash table.