Bubble sort in C is the most straightforward sorting algorithm called a sinking sort, and It works by repeatedly moving the largest elements to the highest index position in the array (if elements are to arranged in ascending order). It requires (n-1) passes to sort an array. For this, it uses several passes through the array and in each pass, the largest element searches its proper position in the sorted array. Bubble sort is not difficult to implement, and it’s fast enough once you have small data sets. The bubble sort algorithm has the same efficiency as the selection sort algorithm.
In Bubble Sort, the first pass starts by comparing the adjacent pair of elements in the array starting at one end and swap (interchange) them if they are not in the proper order (i.e. first and second elements compared and swapped if first is greater than the second). We then move to the next higher position element and repeat this process (i.e. second and third elements are compared and swapped if necessary and so on). This process of comparing and interchanging repeated until the largest element bubbled from its original position to the correct place in the final sorted array. Every time the algorithm moves through the list, it’s known as a ‘pass.’
For sorting an array in ascending order, the first iteration moves the largest value to the last position of the array. As a result, the sufficient size of the array is reduced by 1. In the next pass, the process is repeated for new subarray (i.e. array with 1 less element than the original) until the largest element of this subarray bubbled to its correct position in the array (i.e. highest index position – 1 ). In subsequent passes, this process repeated until the effective size becomes 1, and in that case, the array sorted as all elements reach their respective positions.
 The bubble sort gets its name because elements tend to move up into the appropriate order like bubbles rising to the surface.
The bubble sort gets its name because elements tend to move up into the appropriate order like bubbles rising to the surface.
We’ll be covering the following topics in this tutorial:
Time Complexity of Bubble Sort
The order of growth of the bubble sort algorithm is Quadratic. Bubble sort has a worst-case and average complexity of О(n2) and will only run in its best-case functioning time of O(n) if the list already sorted (best-case), in which n is the number of items sorted. Bubble sort is a stable sort using a space complexity of O(1). Most functional sorting algorithms have considerably better worst-case or average complexity, frequently O(n log n).
The main drawback of bubble sort is time complexity. It’s the slowest algorithm, and it functions with a time complexity of O(n2). Its efficacy declines dramatically when the number of elements in the unsorted list rises.
Pseudocode for Bubble Sort
Here is the pseudo-code of bubble sort.
for i = 0 to n - 1
// to keep track of the number of iterations
for j = 0 to n - 1
// to compare the elements inside the particular iteration
// swap if any element is greater than its adjacent element
if arr[j] < arr[j + 1] then
swap(arr[j], arr[j + 1])
end if
end for
end forBubble Sort Algorithm in C
• Start at index zero, compare the element with another one (a[0] & a[1]), also swap if a[0] > a[1]. Compare a[1] & a[2] and swap if a[1] > a[2]. Repeat this procedure till the end of the array. After doing so, the biggest element is present in conclusion. This entire issue refers to a pass. In the first pass, we procedure array elements from [0,n-1].
• Repeat step one, however procedure array elements [0, n-2] because the previous one, i.e., a[n-1], is present in its proper position. Following this step, the most prominent two elements are found in the end.
• Repeat this procedure n-1 times.
Example:
First Pass:
( 6 2 5 3 9 ) → ( 2 6 5 3 9 ), Here, algorithm compares the first two elements, and swaps since 6 > 2.
( 2 6 5 3 9 ) → ( 2 5 6 3 9 ), Swap since 6 > 5
( 2 4 6 3 9 ) → ( 2 5 3 6 9 ), Swap since 6 > 3
( 2 5 3 6 9 ) → ( 2 5 3 6 9 ), Now, because all elements are already in order (9 > 6), algorithm does not swap them.
Second Pass:
( 2 5 3 6 9 ) → ( 2 5 3 6 9 )
( 2 5 3 6 9 ) → ( 2 3 5 6 ), Swap since 5 > 3
( 2 3 5 6 9 ) → ( 2 3 5 6 9 )
( 2 3 5 6 9 ) → ( 2 3 5 6 9 )
Now, the array already sorted, but our algorithm doesn’t know whether it’s complete. The algorithm requires one full pass with no swap to understand it’s sort.
Third Pass:
( 2 3 5 6 9 ) → ( 2 3 5 6 9 )
( 2 3 5 6 9 ) → ( 2 3 5 6 9 )
( 2 3 5 6 9 ) → ( 2 3 5 6 9 )
( 2 3 5 6 9 ) → ( 2 3 5 6 9 )
In the next program, we’re implementing bubble sort in C language. Within this program, the user would request to put in the number of elements and the element values. Then the program could sort them in ascending order with a bubble sorting algorithm.
Implementing the bubble sort program in C
Here is an example:
(7 5 3 2 4)
When You implement bubble sort, above array will be Flipped to (2 3 4 5 7)
Here is the example of c program for bubble sort
int main() {
int array[100], n, i, j, swap;
printf("Enter number of elements n : ");
scanf("%d", &n);
printf("Enter %d Numbers n :", n);
for(i = 0; i < n; i++)
scanf("%d", &array[i]);
for(i = 0 ; i < n - 1; i++) {
for(j = 0 ; j < n-i-1; j++) {
if(array[j] > array[j+1]) {
swap = array[j];
array[j] = array[j+1];
array[j+1] = swap;
}
}
}
printf("Sorted Array:n");
for(i = 0; i < n; i++)
printf("%d", array[i]);
return 0;
}
Output :
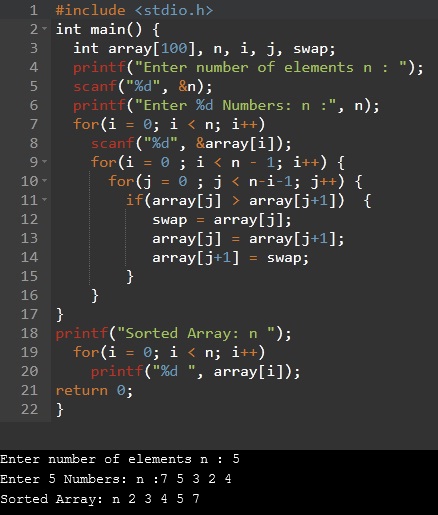 This program provides you a demonstration of the bubble sort algorithm. In the first portion of the code, we take the number of elements in the array and save it. In the following section, the user enters the elements of the array.
This program provides you a demonstration of the bubble sort algorithm. In the first portion of the code, we take the number of elements in the array and save it. In the following section, the user enters the elements of the array.
Then there are two ‘for loops.’ The first ‘for loop’ runs from i value equal to zero until it’s significantly less than n-1. The outer array cares for the element of the value compared with the other elements.
There’s another loop within the loop, which begins from j = 0 to j<n-i-1. This loop takes care of all elements. Inside, there is an if statement that compares if a[j]>a[j+1]. Whether this condition fulfills, then swapping happens. A variable called swap use for this. To begin with, a[j] is assigned to swap, followed with a[j+1] assign at a[j], and last, swap assign into a[j+1]. It continues till all the elements sort—next, the sorted array print.
How can I improve my bubble sort in C?
An improved version of bubble sort, called modified bubble sort, includes a flag that set if an exchange made following an entire pass within the array. If no exchange creates, then it should be evident that the array is already in order because no two elements will need to be changed. If so, the sort ought to end. The new best circumstance order with this algorithm is O(n), as though the array already sorted; subsequently, no exchanges made.
Optimised Bubble sort
Optimized Bubble sort is among the most straightforward sorting methods. Possibly the only advantage it has over other approaches is detecting whether the input is already sorted. It is faster than a different sorted array and consumes less time to describe whether the input array sort or not.
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular