Most computer operations involve manipulation of data stored in various memories. The smallest unit of computer memory is called a bit. When a bit is set its value is taken to be equal to 1 and when it is reset its value is taken to be 0. Thus, a bit can have one of the two values, i.e., 0 or 1. In electronics, memory circuits are called flip-flops. A flip-flop is the name given to a memory circuit which behaves in a manner similar to a switch. When a switch is set on, there is high voltage at its output and it remains on till it is reset ill which case the voltage at its output terminal becomes 0. Similarly, when a flip-flop is set its value is taken as 1 and when it is reset its value becomes 0. One flip-flop represents one bit of memory. The output state can be manipulated according to the input signal to the flip-flop. Since bits are extremely small units of memory, in computer programs we often deal with groups of bits. A group of 8 bits is called a byte.
Let us now proceed to explore the number systems that we would require to deal with while learning more about computer programs. Consider a decimal number 1575 (one thousand five hundred seventy five). How is this number constructed? We are already aware of the place values used in decimal number system, which is – unit’s place, ten’s place, hundred’s place, thousand’s place, and so on. In the given number 1575, 5 occurs at unit’s place, therefore, its value is 5; 7 occurs at ten’s place, so, its value is 70; 5 occurs at hundred’s place, so, its value is 500; and finally, 1 occurs at thousand’s place, so, its value is 1000. The complete number may be composed as shown below.
1575 = 1 x 1000 + 5 x 100 + 7 x 10 + 5 x 1
Thus, apart from the value of the digit, its place value in the number is also important. In the above case, we dealt with the decimal number system in which the place values are multiples or powers of 10. Similarly, in a binary number system, there are only two allowed digits, 0 and 1, and the place values vary as powers of 2. Thus, if we have a number, say 1101, its decimal equivalent will be calculated as illustrated below.
1101=1 x 23+ 1 x 22+0 x 21+ l x 20 = 8 + 4 + 0 + 1=13
From the above example, it is clear that if we have a row of bits, we can easily represent a number in binary form. Figure shows 8 bits (1 byte) using 8 rectangular figures numbered from 0 to 7. In computer terminology, the counting starts from 0 (zero-based .counting). Here, we take the rightmost bit in the figure as the 0thbit at the unit’s place. The digit in this position has the place value 20= 1. The next flip flop (shown by rectangle at l) occurs at a place where the place value is 21 = 2. The next bit (third from right) has a place value of 22= 4 and so on. The last position has the place value 27= 128. Now, if the bits numbered 0, 1, 3, 4, 6, and 7 are set (each equal to 1) and bits 2 and 5 are 0, then the number stored is 219 as explained in Fig. If all the bits are set as high (i.e., 1) they represent the number 255, and when all of them are set as low, they represent 0. So, a set of 8 memory bits (or one byte) can hold any number from 0 to 255 or from 0 to (28– 1). 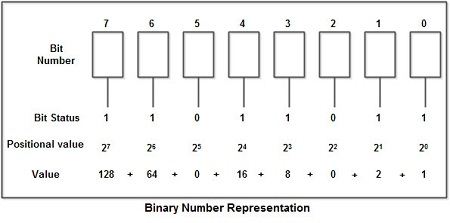
Consider that we have two bytes to represent our number (as shown in Fig), if all of them are 0 the number stored is 0 and if all of them are set (1) the value stored is 216 – 1= 65535. So, any positive number in the range from 0 to 65535 may be stored using two bytes of memory. 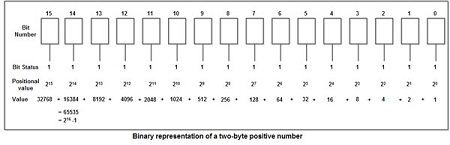
So, the basic working of a computer may be understood as follows: In a computer, all objects are represented by numbers in binary form, whether they are digits, letters, or operators. A computer can easily manipulate them and output a result in the form of a binary number which is then coded into decimal numbers and letters and displayed on the monitor or printed using a printer.
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular