C calculating Integration using Trapezoidal Rule

The trapezoidal rule is the simplest method to approximate the definite integral of a function f(x) over the interval [a, b]. Given N equally space points (with a spacing of h) X0, X1, …, XN such that X0 = a and XN = b, the integral of f(x) can be approximated as the sum.

(X0/2=X1+X2+……+Xn-1+Xn/2)

The program TRAPEZOID.C integrates a function whose pointer is passed to it using the trapezoidal rule.

#include <stdlib.h> 
 #include <math.h> 
 #include <stdio.h> 
 /* function prototypes */ 
 double integrate(double(*func)(double), 
 double xa, double xb, int intervals); 
 double foobar(double x); 
 double myfunc(double x); 
  double foobar(double x) 
  { 
      return (exp(x)-2.0); 
  } 
    double myfunc(double x) 
   { 
     return x*x; 
   } 
                double integrate(double(*yfunc)(double), 
      double xa, double xb, int nintervals) 
      { 
                 double sum=0.0, x, hwidth; 
                 int iter; 
                 x = xa; 
                 hwidth = (xb-xa)/nintervals; 
             for(iter=0;iter<nintervals-1;iter++) 
             { 
                 x+= hwidth; 
                 sum+= yfunc(x); 
             } 
                    sum+= yfunc(xa)/2.0; 
                    sum+= yfunc(xb)/2.0; 
                    return sum*hwidth; 
      } 
 int main() 
 { 
        double integral, pi; 
        clrscr(); 
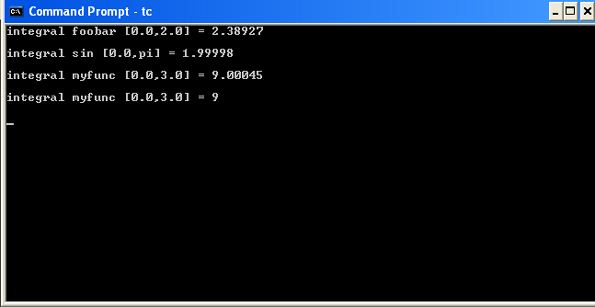
        integral=integrate(foobar,0.0,2.0,100); 
        printf("integral foobar [0.0,2.0] = %lg\n\n",integral); 
        pi = acos(-1.0) ; 
        integral=integrate(sin,0.0,pi ,300); 
        printf("integral sin [0.0,pi] = %lg\n\n",integral); 
        integral=integrate(myfunc,0.0,3.0,100); 
        printf("integral myfunc [0.0,3.0] = %lg\n\n",integral); 
        integral=integrate(myfunc,0.0,3.0,1000); 
             printf("integral myfunc [0.0,3.0] = %lg\n\n",integral); 
               return 0; 
               getch(); 
 }