Merge Sort in C

Merge Sort in C is a divide and conquer algorithm which John von Neumann developed in 1945. We divide the data into smaller pieces, recursively conquer each piece and merge the result into the final result until the original list is rebuild sorted. This tutorial will help you to understand Merge Sort In C in detail.

What is Merge sort in C?

Merge sort uses divide and conquer to sort a particular array. In Merge sort, the original array is subdivided into a “nearly” equal-sized array. Then two sub-arrays are sorted separately. The two-sorted sub-arrays are then merged into a single sorted array through merging methods. Hence the name Merge Sort is given to this technique.

We keep splitting each of the sub-arrays till each sub-array contains just one item. A sub-array containing one item needs no sorting.

Merge sort is a comparison based stable algorithm. It requires less time to sort a partially sorted array. The complexity of the merge sort algorithm is O(n log n).

In-place, top-down, and bottom-up merge sort are different variants of merge sort.

Merge Sort Methods

Merge Sort is generally regarded as one of the best internal sorting methods. If the data is too large to be stored simultaneously in the memory, external sorting methods should be used. Small data blocks are loaded into the memory, sorted by an internal sorting method, and written out to a disc in external sorting methods. Sorted parts are then merged with merging algorithm variations.

Divide & Conquer algorithm has 3 steps:

1. Divide: Breaking the list into n sublists.
2. Conquer: Recursively splits the list.
3. Merge: Merges those sublists to produce a sorted list.

Merge sort is one of the most potent and quick sorting algorithms with the following time complexity

Time Complexity of Merge Sort in C

The complexity of the merge sort in every case is O (n log₂ n). To understand we derive this time complexity for merge sort, two factors need to be considered.

(a) Number of recursive calls.
(b) Time is taken to merge each sub-array.

To understand the first factor, consider an array of n elements where n=2^k where k>0. The initial call to MERGESORT () algorithm makes two recursive calls to it, dividing the array into two sub-arrays of n/2 elements. Moreover, each of the two recursive calls to MERGESORT() makes two further recursive calls to MERGESORT (), dividing the two sub-arrays into four sub-arrays of n/2² or n/4 elements each. This process continues, and the final recursive call (k^th level) divides the sub-array into n sub-arrays of 1 (n/2^k)element each. It takes k levels (log₂n where n = 2^k) of recursive calls to obtain n sub-arrays of one element. Thus complexity for the recursive call is O(log²n).
Now consider the other factor. The merge process makes at most (n – 1) comparisons among n elements in the two sub arrays. Each merge also requires n moves to a temporary array and n moves back to the original array. In total, each merge requires at most 3n – 1 operation, i.e. O(n).
Therefore, the overall complexity of the merge sort is O(n log₂ n).

Merge Sort Algorithm

MergeSort(arr[], left, right), Where left is the first indexed 
element & right is the last indexed element in the list. 
if right > left
1. Select the middle array index to break into two sublists : 
   middle = (left + right)/2
2. Call MergeSort for first sublist : 
   mergeSort(array, left, middle)
3. Call mergeSort for second sublist : 
   mergeSort(array, middle +1, right)
4. Recursively, merge two sublists in a sorted style, 
   leaving just one sorted array. : merge(array, left, middle, right)

Example:

1. Divide the unsorted list recursively until there is only one element remaining.

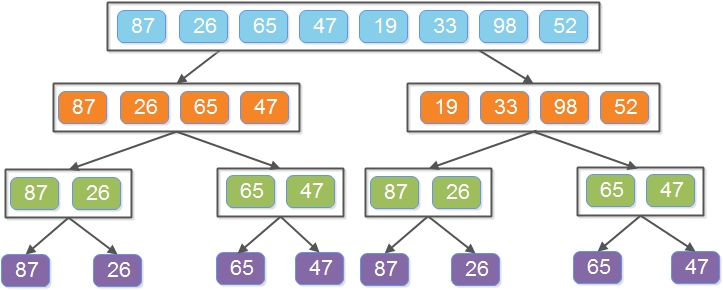
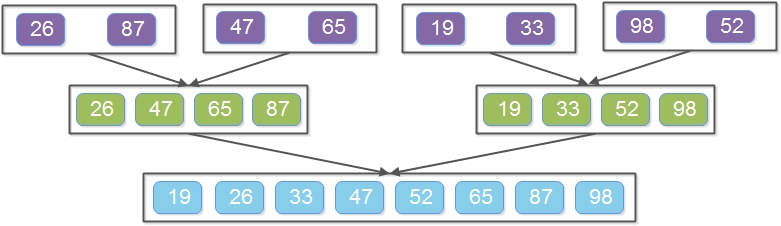
2. Merge sublists recursively to produce sorted sublists until all the sublists merge and there is only one list left.

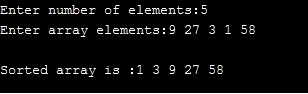
C Program For Merge Sort

#include<stdio.h>
void mergesort(int a[],int l,int r);
void merge(int a[],int l1,int r1,int l2,int r2);
int main() {
 int a[30],n,l;
 printf("Enter number of elements:");
 scanf("%d",&n);
 printf("Enter array elements:");
 for(l=0;l<n;l++)
   scanf("%d",&a[l]);
   mergesort(a,0,n-1);
   printf("\nSorted array is :");
   for(l=0;l<n;l++)
     printf("%d ",a[l]);
     return 0;
}
void mergesort(int a[],int l,int r) {
 int mid;
 if(l<r) {
   mid=(l+r)/2;
   mergesort(a,l,mid); //left recursion
   mergesort(a,mid+1,r); //right recursion
   merge(a,l,mid,mid+1,r); //merging of two sorted sub-arrays
 }
}
void merge(int a[],int l1,int r1,int l2,int r2) {
 int temp[50]; //array used for merging
 int l,r,k;
 l=l1; //beginning of the first list
 r=l2; //beginning of the second list
 k=0;
 while(l<=r1 && r<=r2) //while elements in both lists {
   if(a[l]<a[r])
      temp[k++]=a[l++];
   else
      temp[k++]=a[r++];
}
 while(l<=r1) //copy remaining elements of the first list
   temp[k++]=a[l++];
   while(r<=r2) //copy remaining elements of the second list
     temp[k++]=a[r++];
     //Transfer elements from temp[] back to a[]
     for(l=l1,r=0;l<=r2;l++,r++)
       a[l]=temp[r];
}