Bitwise Operators in C

All the objects stored in a computer are ultimately converted into binary numbers, sequences of 0s and 1s. Each digit in a binary number store on one bit of the computer memory. A bit define as the smallest unit of memory in a computer. The computer manipulates a number by manipulating the bits on which the number stored. In control systems also we often need to use operators to manage bits.

The Bitwise operators in C also called bit-level programming used for manipulating individual bits in an operand. Bit by bit works on one or several bit patterns or binary numerals at the individual bit level. It is used in numerical calculations to speed up the process of computation. It is used extensively in embedded software. 

The C language provides six bitwise operators to manipulate the bit patterns of integral values (integers and characters). They include not, i.e., complement(~), and (&), or (|), exclusive or, i. e., xor (^), left shift (<<) and right shift (>> ). These operators work directly on the bit patterns of the operands, i. e., on sequences of bits (0 and 1) representing the operands. In addition, C language provides five compound assignment operators (&=,| =, ^=, <<= and >>=).

The complement operator (~) is a unary prefix operator and is used, as in ~a, whereas all other operators are binary infix operators and used as in a op b.

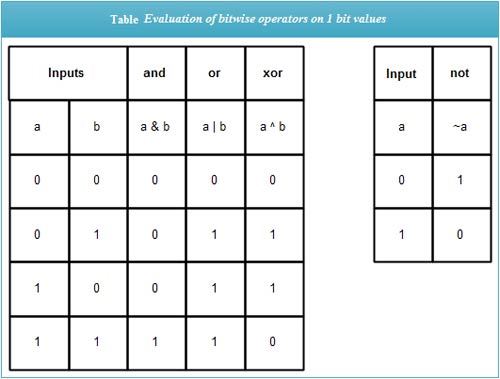
First, consider these bitwise operations on individual bits. The bitwise and operator evaluates as 1 if both operands are 1, and zero otherwise. The bitwise or operator evaluates as 1 if either or both operands is 1, and zero otherwise. The bitwise xor operator evaluates as 1 if either of the operands (but not both) is 1, and zero otherwise. Finally, the bitwise not operator complements the operand’s value, i. e., and it returns 1 if the operand is zero and vice versa. These operations summarize in Table.

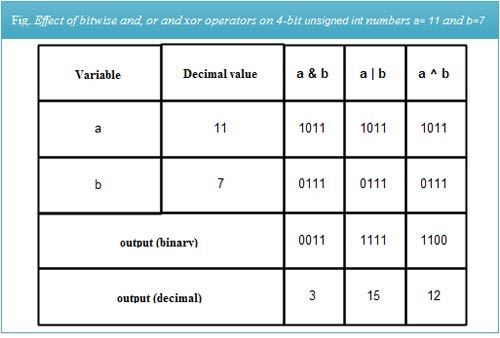
While working with integral numbers, the bitwise operations performed on all bits. As we know, char values represented using 1 byte (i. e., 8 bits), int values using either 2 or 4 bytes, short int using 2 bytes, and long int using 4 bytes. These values may be signed or unsigned. However, binary operators’ working illustrated here using 4-bit numbers a and b having decimal values 11 (binary 1011) and 7 (binary 0111), respectively.

The bitwise and, or and xor operations performed on corresponding bits of two integer operands by applying bit operations, as shown in Table. Thus, a & b (i. e., 1011 & 0111) evaluates as 0011, i.e., decimal 3 as shown in Fig. Also, a | b evaluates as 1111(decimal 15), and a ^ b evaluates as 1100 (decimal 12).

The complement operation performs on all the bits of a number. Thus, the expression ~a evaluates as 0100 (decimal 4). This complement operation is also called 1’s complement. The left shift (<<)and right shift (>>) are binary infix operators used, as in val << n and val >>n. They shift the bits in the first operand (val) by several bit positions specified in the second operand (n).

When a value shifted left, the empty bit positions on the right filled with 0 bits; the bits that move out of the number are lost. Thus, expression a << 1 left-shifts bit in variable a (binary 1011) by 1-bit position to obtain 0110. (decimal 6) and expression a << 2 left-shifts bits in variable a by 2-bit positions to get 1100 (decimal 12) as shown in Fig.

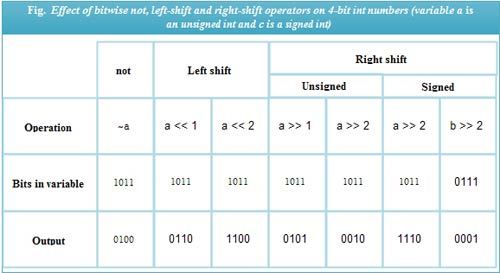
The working of the right shift operator depends on whether the number shifted is signed or unsigned. When an unsigned number shifted to the right, the empty bit positions on the left (i. e., MS bits) filled with 0 bits. This shift is called the logical right shift. Also, note that the bits that move out of a number are lost. For example, assuming that variable a (binary 1011) is an unsigned int variable, the expression a>> 1 evaluates as 0101 (decimal 5) and a>> 2 as 0010 (decimal 2).

When a signed int shifted to the right, the bits shifted as usual, except that the MS bit copied to itself. Thus, the empty MS bit positions all become equal to the sign bit. This shift is called the arithmetic right shift. For example, assuming a (binary 1011) and b (binary 0111) to be signed int variables, the expression a >> 2 evaluates as 1110, and expression b >> 2 evaluates as 0001.

Observe that a right shift by 1-bit position is equivalent to integer division by 2. Also, a left shift by 1-bit position is equivalent to multiplication by 2, provided the most significant bit of the number shifted is 0.

The bitwise compound assignment operators are similar to other compound assignment operators. For example, the assignment expression a & = expr is equivalent to the expression a= a & (expr).

Precedence and Associativity of Bitwise Operators

The bitwise complement operator is a unary operator and has the precedence and associativity as other unary operators. Thus, its precedence is higher than the arithmetic operators, and it has right-to-left associativity.

All other bitwise operators have left-to-right associativity. The precedence of the bitwise shift operators is just below that of the arithmetic operators and higher than that of the relational operators. The bitwise and, xor and or operators have precedence (in that order) below that of the equality operators (== and ! =) and above that of the logical operators (&& and ||).

Finally, the bitwise compound assignment operators ( &=, ^=, |=, <<= and >>=) have the precedence and associativity as other assignment operators. Thus, they have precedence below that of the conditional operator (? 🙂 and above that of the comma operator (,) and right-to-left associativity.

Set, Reset and Complement a Specific Bit

Let us now understand how we can set, reset, or complement a specific bit at position pin a given number without affecting other bits in it. For this, we need to perform a particular bitwise operation between the given number and another value called a mask.

The mask should usually have the same size in bits as that of the number operated. One of two masks will use depending on the operations to perform. One mask has 1 bit at position p and 0 bit at all other positions, and another mask with 0 bit at position p and 1 bit at all other positions. For example, for operations on bit position 2, we require either 0000 0100 or 1111 1011 as the mask.

These masks can quickly obtain using the bitwise left shift operation on number 1, which has a bit pattern of 0000 0001, i.e., 1 bit at bit position 0 and 0 bit at all other positions. Thus, to obtain a mask with 1 at bit position p and 0 at all other positions, we use the expression 1<< p. We can complement this mask to obtain a mask with 0 at bit position p and 1 at all other positions using the expression ~ (1<< p).

Now, to set a bit at position p in a given number num, without affecting other bits in it, we use the bitwise or value of a with a mask having bit 1 at position p and 0 at all other positions, as shown in Fig, using the following statement.

num = num | (1 << p);

Note that the parentheses in the above expression are redundant but they improve readability. Alternatively, we can use the compound assignment operator |= as shown below.

num | = 1 << p; /* set bit at position p */

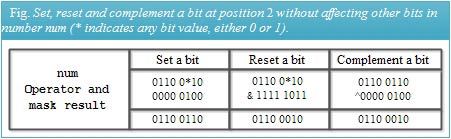
We can use the above mask and the bitwise xor operator to complement (toggle) a bit at Position p without affecting the other bits as

num ^ = 1 << p; /* complement bit at position p */

To reset a bit at position p without affecting the other bits in a given number num, we need to perform a bitwise and operation between num and the mask having 0 bit at position p and 1 at all other positions using the following statement.

num &=~(1 << p); /* reset bit at position p */

Testing Bits

To test the value of a bit at position p in number num, we check the condition num & (1<< p). If this expression is non-zero, the bit at position p set; otherwise, it is 0.

We can perform this test on all bits of a given number num using a loop, as shown below.

Note that the parentheses in the test for the statement are essential as the > operator has higher precedence than the & operator. Alternatively, we can write this test simply as

if (num & mask)

If the mask has same size (in bits) as that of num, we can alternatively write the above for loop in a concise manner by eliminating loop variable bas shown below.

for(mask = 1; mask > 0; mask<<= 1) {  
 if (num & mask) {  
  /* bit b is 0, perform desired operation */  
}  
 else { 
  /* bit b is 1, perform desired operation */  
 } 
}

Sometimes we may wish to process the bits in a given number from left to right. For this, we need to take a mask with a 1 bit in the MS bit position and 0 at all other bit positions. This can be achieved by shifting number 1 left as shown below.

mask= 1 << (8 * sizeof(mask) - 1)

Note that to shift this bit right one bit position at a time, we have to use a logical right shift operation in which the empty MS bit positions created by the right shift are set to 0. Hence, mask should be declared as an unsigned variable.

Example of test the bits in a number

a) Count the number of zeros and ones in a binary representation of a number

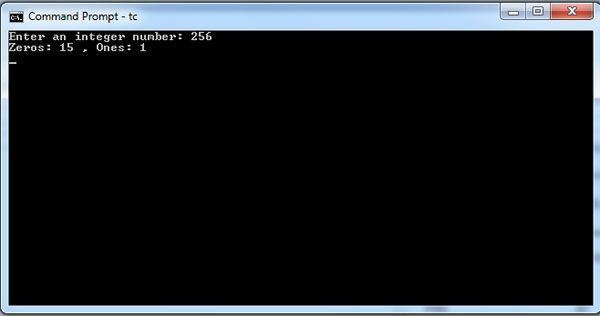
A program to count zeros and ones in a binary representation of a number is given below.

#include<stdio.h>
int main() {
 int num;
 int zeros, ones;
 int b, mask;
 printf("Enter an integer number: ");
 scanf ("%d",&num);
 ones = 0;
 mask = 1;
 for(b = 0; b < 8 * sizeof(num); b++) {
  if (num & mask)
    ones++;
    mask <<= 1;
 }
  zeros= 8 * sizeof(num) - ones;
  printf("Zeros: %d Ones: %d\n", zeros, ones);
  return 0;
} 

We can also write a function count_lbits to count the number of ones in the binary representation of a number as shown below.

int count lbits(int num) {
int ones, mask;
ones = 0;
for(mask = 1; mask > 0; mask<<= 1) {
  if (num & mask)
    ones++;
}
 return ones;
}