Procedure to Create a Program in C Programming Language

There are many “languages” like, for example C, Fortran, PASCAL etc., that help us to convert an algorithm in to something that a computer can understand. We will focus here only on C programming So. let us start looking at how do we create a “C program”.

There are basically three steps involved in converting your ideas into what is to be done to make it a working program.  There are three steps involved in converting your idea of what is to be done to a working program.

1. Creating a source code in the form of the text file acceptable to the compiler.
2. Invoking the compiler to process the source code and produce an object file.
3. Linking all the object files and libraries to produce an executable 16.

We will look at these parts in some more detail here.

The source code is where you express the the whole computation you want to do into a series of instructions.

The tradition is to use the C source code with an extension .c For example myfile.c . Some compilers insist on this extension. This is an acsii file that you can create using any one of the editors that you are familiar with. We will look at the detailed structure of this code in a little while .

We may have different parts of the code in different files. We then compile them separately or together to form object files. During this operation the compiler checks and convert your source code to a language understandable to the particular processor that is used in the computer. These object files that comes with an extension .o, for example myfile.o , are in binary format.

The next step is to link these object files and other libraries and header files etc., to produce an executable. This executable file contains a set of instruction in a language that the processor can understand and is the one which we run on the computer. We will see the use of header files and system libraries in the examples given below.

Before proceed let us summarize the steps that takes us to run a program in the form of a flow chart.

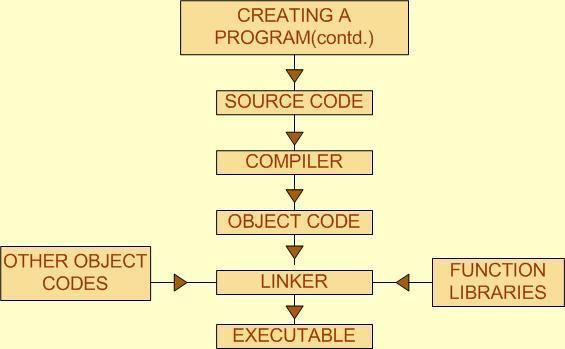
As we said earlier it is the tradition to write a C program file name ending with the extension .C.

Example: Below we give a program that computes the square root of a number and prints it on the scree. Since it is a C program we name it as “myfile.c” , that is with an extension “.c”.

#include 
#include 
main()
{       
            float x,y;       
                   scanf("%f\n",&x);       
            y=sqrt(x);  
                   printf("%f\n",y); 
} 

Before we proceed to the compilation of this program let us take a minute to see what does each of the lines mean?

Lines 1 and 2 are header files. These files contain the math library functions and the input output command functions. We need the math function library to use functions like “sqrt”, “log”, “power” etc. We need the stdio library to use functions like “scanf” and “printf” which reads and prints the data from the screen. More on this a little later.

The program given above just has a main body. Line 3 is declares the starting on this part. The lines inside the { } following this are the part of the main program.

Line 4 is the declaration of the variables. Again we will see more on the variable types later in this course. In this particular example we declare variables “x,y” as floating points.

Line 5 reads the value of the variable from the screen.

Line 6 computes the square root of the variable “x” and put the value into variable “y”.

Line 7 prints out this value of y.

We first compile this code to produce an object code using the command cc -c myfile.c or an equivalent command available at your machine.

The object file produced by this, myfile.o is then linked with the system math library using the command, cc -lm myfile.o -o myfile.exe , to produce the executable myfile.exe.

(the second term in the command above “-lm” links the object file to the math library. The file name that comes just after -o is the name of the executable).

We can combine compile and link into one step as will see in later part of the course.

Example: Let us now look at a C program that uses the library and another function.

#include 
#include 
main() 
{         
   float x,y;         
   printf ("%f\n",&x);         
   y=sqrt(x);         
   printf("%f\n",y);          
   printf("The program is Over"); 
} 

This simple C code adds an additional component to the one we saw earlier, it calls a function “printit”. As before you can see the “include” files, or what are called header files. Then we will see the main part of the program. This program is basically computing square root of the variable x and it is printing it out on the screen.

Then it is calling some function, which prints out a statement.Here we see on of the main feature of a C program. The main part does some of the calculations and it calls another function. The function we called, named printit, which simply prints the sentence “the program is over.” can be put it a separate file. Let is call it “print.c”. We will see that how it can be compiled and how it can be executed.There are two ways to compile this program.

To compile these programs we could type cc -c sample.c and cc -c print.c separately.This commands will create sample.o and print.o files. We can create the executable by typing the command.cc sample.o print.o -lm -o a.out In this linking command we have put together the two files and also included the math library file m.a We can now execute the program by typing a.out.You could try variations of these commands and programs to figure out why we need the math.h file and why we need to include -lm in the linker etc.

Also try it for different math functions, for example calculating the logarithm or trigonometric functions etc.Another way to compile and generate an executable from this is to simply type cc sample.c print.c -lm -o a.out In this the compilation and linking is put together.Let us try another program to illustrate the use of math library and the compilation and linking procedure.