Two-dimensional Arrays or Matrices in C

A two-dimensional array (commonly called a matrix) consists of elements of the same type arranged in rows and columns. The rows and columns of a matrix are numbered starting from 0. Thus, for an array of size rows x cols, the row subscripts are in the range 0 to rows – 1 and the column subscripts are in the range 0 to cols – 1.

Declaration

The declaration of a two-dimensional array takes the following form:

arr_type arr_name [ rows ] [ cols ] ;

where arr_name is the name of the array being declared, each element of which is of type arr_type. The expressions rows and cols enclosed in square brackets are constant integral expressions (or integral constants) that specify the number of rows and columns in the array. When a compiler comes across the declaration of an array, it reserves memory for the specified number of array elements. For a two-dimensional array, the memory required is given as rows* cols* sizeof(arr_type).

Note that we can declare matrices of built-in as well as user-defined types; we can also declare multiple matrices in a single declaration statement, separated by commas. Scalar variables, vectors and multidimensional arrays can also be declared along with matrices.

Accessing Matrix Elements

An element of a matrix can be accessed by writing the array name followed by row and column subscript expressions within separate array subscript operators as shown below.

arr_ name [ row_expr ] [ col_expr ]

where row_ expr and col_ expr are integral expressions that specify the row and column positions, respectively, of an element in the array. As mentioned earlier, for an element access to be valid, the values of row_ expr should be in the range 0 to rows – 1 and the values of col_ expr should be in the range 0 to cols – 1.

Operations on Matrix Elements

We can perform various operations on the elements of a matrix, similar to those for scalar variables and elements of a vector. For a matrix of any built-in type, we can use its elements in an expression, assign a value to it, perform increment and decrement operations, pass it as an argument to a function and so on. In particular, the prefix and postfix increment (and decrement) operators and the address of operator can be used as follows:

++arr_name [row] [col]
arr_name [row] [col]++
&arr_name [ row ] [ col ]

In these expressions, the array subscript operators are bound first to their operands followed by the ++ and & operators. Thus, parentheses are not required in these expressions.

Operations on Entire Matrices

As with vectors, C does not provide any statements or operators to perform operations on an entire two-dimensional array. Nested for loops are usually used to perform operations on an entire array as illustrated below for a two-dimensional array a of size m x n:

for (i = 0; i <; m; i++) {
  for (j = 0; j < n; j++) {
   /* process element a[i] [j] */
  }
}

The index variable i (of the outer for loop) assumes the values 0, 1, … , m – 1. For each value of i, the index variable of the inner for loop (j) assumes the values 0, 1, … , n – 1. Thus, the use of the expression a [i] [j] causes the elements to be accessed in row-wise manner in the order a [0] [0], a [0] [1], … , a [0] [n-1 ], a [1] [0], a [1] [1], … , a [ 1 ] [9], … , a [m-1] [0], a [m-1] [l], … ,a [m-1] [n-1]. Note that we can use the expression a [j] [i] to access array elements in a column-wise manner.

Initialization

A matrix can be initialized using a syntax similar to that used for the initialization of vectors. Thus, the declaration

int mat [3] [4] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 };

declares an integer matrix mat of size 3 x 4 and initializes it in a row-wise manner as shown in Fig. The readability of this initialization statement can be greatly improved by writing the initialization list in the form of a 3 x 4 matrix as shown below:

int mat[3] [4] = {
 1, 2, 3, 4,
 5, 6, 7, 8,
 9, 10, 11, 12
};

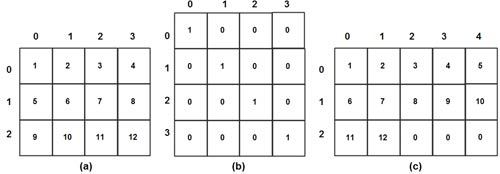
Similarly, the following declaration initializes an integer unit matrix of size 4 x 4 as shown in Fig.

int unit_mat[4] [4] = {
 1, 0, 0, 0,
 0, 1, 0, 0,
 0, 0' 1, 0'
 0, 0, 0, 1
} ;

It is possible to omit the first dimension (i. e., the number of rows) of a two-dimensional array in an initialization statement. The number of rows in the matrix is determined from the number of elements specified in the initialization list. Consider the example given below.

int x[] [5] = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12);

This initialization statement declares an array x with five elements in each row and initializes it with 12 elements. Thus, the number of rows is determined as [12/5], i. e., 3. Moreover, as the initialization list does not specify the values for the last three elements in the third row, they are initialized to 0. Thus, the array x is initialized as shown in Fig

C language allows the initialization list for each row to be enclosed within a pair of braces. Thus, the declaration of array mat given above can alternatively be written as follows:

int mat[3] [4] = {{l, 2, 3, 4), {5, 6, 7, 8), {9, 10, 11, 12}};

Observe that the initialization lists for different rows are separated by commas. The initialization list for each row is usually written on a separate line to improve readability as shown below.

int mat[3] [4] = {{ 1, 2, 3, 4},{ 5, 6, 7, 8} ,{ 9, 10, 11, 12)} ;

Note that if the initialization list for a row of a matrix contains fewer values than required, the remaining elements in that row are initialized to the default value, which is 0 for arithmetic data types. Thus, the initialization of array unit_ mat declared above can also be declared as follows:

int unit_mat[4] [4] = {{1}, {0,1), {0,0,1), {0,0,0,1}};

Finally note that if the initialization list for the entire array or one of its row contains more elements than required, the compiler gives a Too many initializers error.

Matrices as Function Parameters

we can pass one or more arrays as parameters to a function. These array parameters can be of different dimensions and types. Moreover, we can mix the scalar and array parameters. We can thus define functions having one or more matrices as parameters. A function that has one matrix parameter is defined as

ret_type func_name(mat_type mat_name [rows] [cols]) {
  /*process matrix mat_name*/
}

The function func_ name takes a matrix mat_ name of type mat_ type and size rows x cols as a parameter and returns a value of type ret_type. Note that the first array dimension in the above definition (i.e., rows) is optional and can be omitted. However, we cannot omit the second dimension. Thus, the above function definition can also be written as shown below.

ret_type func_name(mat_type mat_name [] [cols]) { ... }

The argument array specified in a call to this function can have any number of rows but it should have cols number of columns, the same as that of the parameter array. However, if the ‘number of columns is different, the compiler gives either a warning message or an error. For example, TC++ gives a warning (Suspicious pointer conversion) and allows program

execution giving wrong results due to different interpretation of data in the argument matrix. Thus, a programmer should be careful particularly while passing matrices (and multidimensional arrays) using old compilers like TC/TC++. The Code::Blocks, on the other hand, reports an error (Passing argument 1 from incompatible pointer type) and does not allow program execution.

The function given above can be generalized to process matrices of different sizes by including two integer parameters, say m and n, that specify the actual size of the matrix (number of rows and columns, respectively) to be processed from the argument array. However, note that the maximum number of columns in the argument array in a function call should still match those in the parameter array in the function definition.

As we know, the operations on a matrix typically consist of performing the same or a similar operation on each of its element. Thus, a function that operates on the entire matrix typically uses a nested for loop as shown below.

void imat_func(int mat[] [10], int m, int n) {
 int i, j;
 for (i = O; i < m; i++) {
   for (j = O; j < n; j++) {
     /* operate on mat(i] [j) */
   }
 }
}

Some calls to this function are shown below.

int main () {
 int a[10] [10), b[5) [10], c[20] [10], d[10] (5];
 imat_func(a, 10, 10); /* ok */
 imat_func(b, 3, 4) ; /* ok */
 imat_func(c, 15, 10) ; /* ok */
 imat_func(d, 5, 5) ;
 imat_func(b, 7, 4) ;
 return O;
}

Recall that for efficiency reasons (to avoid unnecessary copying of an entire array when a function is called), C language uses the call by reference mechanism to pass arrays. In this mechanism, only the starting address of array argument is passed to the called function. This makes an array an input-output parameter. When the function modifies elements of the parameter array, it actually modifies the elements of the argument array in the called function. Thus, the modified array is available in the calling function. If this behavior is not desirable, we can use a const array or a pointer to a const mechanism.