C Program for GCD using Euclid’s algorithm

Let us use variables m and n to represent two integer numbers and variable r to represent the remainder of their division, i. e., r = m % n. Euclid’s algorithm to determine the GCD of two numbers m and n is given below and its action is illustrated form= 50 and n = 35.

while (n > 0) {
   int r = m % n;
   m = n;
   n = r;
    }

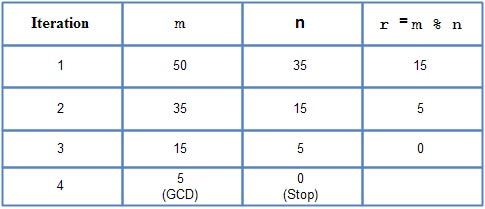
In each iteration of this loop, we determine the remainder (r = m % n) and assign current values of variables n and r to variables m and n, respectively. Execution is continued as long as the value of divisor n is greater than zero. When the value of n becomes zero, the value of variable m is the GCD of the given numbers as indicated above. The complete program is given below.

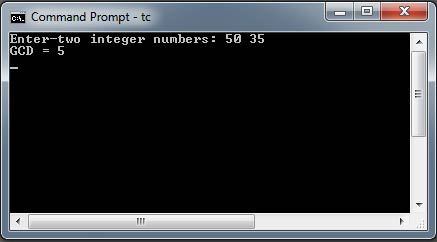
/* GCD of two numbers using Euclid's algorithm*/
#include <stdio.h>
void main() {
    int m, n; /* given numbers */
    clrscr();
    printf("Enter-two integer numbers: ");
    scanf ("%d %d", &m, &n);
    while (n > 0) {
        int r = m % n;
        m = n;
        n = r;
    }
    printf ("GCD = %d \n",m);
    getch();
}