To eliminate these anomalies in 3NF relations, it is necessary to carry out the normalization process to the next higher step, the Boyce-Codd Normal Form.
BCNF is simply a stronger definition of 3NF. Since BCNF is higher form of 3NF, so a relation in BCNF must be in 3NF. BCNF makes no explicit reference to first and second normal form as such, nor the concept of full and transitive dependence.
We’ll be covering the following topics in this tutorial:
BCNF states that:
• A relation R is in Boyce/Codd N/F (BCNF) if and only if every determinant is a candidate key. Here, determinant is a simple attribute or composite attribute on which some other attributes is fully functionally dependent.
For example: Qty is FFD on (Sno, Pno)
(Sno, Pno) → Qty, here(Sno, Pno) is a composite determinant.
Sno → SnameHere, Sno is simple attribute determinate.
Similarities between 3NF and BCNF
The relations which are achieved after application of 3NF can also be achieved by BCNF.
For example, relation Course_Student and Student_System_Charge which are not in 3NF are also not in BCNF.
Course Student
(Course _Code, Rollno, Name, System _Used, Hourly _Rate, Total_Hours) Here, (Course_Code, RoIIno) ----+ Total_Hours RoIIno → Name | System_Used | Hourly_RateHere, Rollno is a determinant but not candidate key (candidate key is course_code, Rollno) so relation COURSE_STUDENT is not in BCNF.
In relation Student_System_Charge
(Rollno, Name, System _Used, Hourly_Rate) Rollno → Name | System_Used | Hourly_Rate System_Used → Hourly_RateHere, System_Used is also a determinant but it is not unique, so relation
Student_System_Charge is not in BCNF.
Now, Consider Course,Hour_Assigned, Student_System_Charge relations which are in 3NF.
Course (Course _Code, Course _Name, Teacher_Name) Hour_Assigned (Course_Code, RoIIno, Total_Hours) Student_System (Rollno, Name, System_Used) Charge (System _Used, Hourly _Rate)These relations are also in BCNF, because
Course_Code → Course_Name | Teacher_Name (In relation Course) (Course _Code, Rollno) → Total_ Hours (In relation Hour_Assigned) Rollno → Name | System_Used (In relation Student_System) System_Used → Hourly_Rate (In relation Charges)Here, each determinant is unique in its corresponding relation.
In conclusion, we can say that in these relations which have only single candidate key can be normalized both with 3NF and BCNF without any problem.
Differences in 3NF and BCNF
In order to show the difference between 3NF and BCNF, relations having overlapping of candidate keys are considered in detail.
Overlapping of Candidate keys
Two candidate keys overlap if they involve two or more attributes each and have an attribute in common.
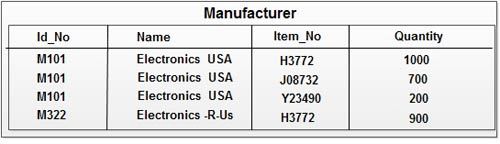
For example, in Manufacturer relation.
Manufacturer (Id_no,Name,Item_No,Quantity)
Here, Name is considered unique for each Id_No.
FD of above relation is
(Id_No, Item_No) → Quantity (Name, Item_No) → Quantity Id No → Name Name → Id_NoThis relation has two overlapping candidate keys, because there are two composite candidate keys (Id_No, Item_No) and (Name,Item_No) out of which Item_No is common attribute in both the candidate keys, so this is a case of overlapping of candidate keys.
Possible FD diagram of this case is:
Here, both the relations are in 3NF, because every non-key attribute is non-transitively fully functional dependent on the primary key.
In above relation, there is only one non-key attribute i.e. Quantity and it is FFD and non transitively dependent on the primary key.
Names, Id_No are not non-key attributes because they can participate into the primary key as shown in FD diagram.
But, Manufacturer relation IS not III BCNF because this relation has four determinants
(Id-no, Item-No) [Qty depends on this combination] (Name,Item_No) [Qty depends on this combination] Id No [Name depends on Id_No] Name [Id_No depends on Name]Out of these four determinants two determinants (Id_No, Item_No) and (Name,Item_No) are unique but Id_No and Name determinants are not candidate keys.
In order to make this relation in BCNF we non-loss decompose this relation in two projections ID_NAME (Id_No, Name) and ID_QTY (Id_No, Item_No, Quantity).
ID_NAME relation has two determinants Id_No, Name and both are unique.
ID_QTY has one determinant (Id_No, Item_No) and is also unique.
These two relations ID_NAME and ID_QTY removes all anomalies of Manufacturer relation.
Another Example
For example, consider a relation
SSP (Sno, Sname, Pno, Qty)Here, Sname is considered unique for each Sno.
FD of above relation is
(Sno, Pno) - Qty (Sname, Pno) - Qty Sno - Sname Sname - SnoThis relation has two overlapping candidate keys, because there are two composite candidate keys (Sno, Pno) and (Sname, PNo) out of which Pno is common attribute in both the candidate keys, so this is due case of overlapping of candidate keys.
Possible FD diagram of this case is:
Here, both the relations are in 3NF, because every non-key attribute is non-transitively fully functional dependent on the primary key.
In above relation, there is only one non-key attribute i.e. Qty and it is FFD and non transitively dependent on the primary key.
Sname, Sno are not non-key attributes because they can participate into the primary key as shown in FD diagram.
But, SSP relation is not in BCNF because this relation has four determinants:
(Sno, Pno) (Sname, Pno) (Sno) (Sname)Out of these four determinants two determinants (Sno, Pno) and (Sname, Pno) are unique but Sno and Sname determinants are not candidate keys.
In order to make this relation in BCNF we non-loss decompose this relation in two projections SN (Sno, Sname) and SP (Sno, Pno, Qty).
SN relation has two determinants Sno, Sname and both are unique.
SP has one determinant (Sno, Pno) and is also unique.
These two relations (SN, SP) remove all anomalies of SSP relation.
Another Case:
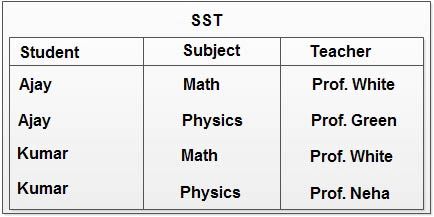
Consider a relation SST with attributes (Student, Subject, Teacher).
There ‘are following rules applied on above relation:
• For each subject, each student of that subject is taught by only one teacher
• Each teacher teaches only one subject
• Each subject is taught by several teachers
Table shows a sample data:
FD’s of above relation are
According to condition 1:
Subject, Student combination gives only one teacher
(Subject, Student) --- TeacherAccording to, condition 2:
Each teacher teaches only one subject
Teacher --- SubjectSince, each teacher teaches only one subject, so a student can taught one subject by only one teacher. In other words, the combination of teacher and student can “also determine subject.
(Teacher, Student) --- SubjectOnce again the relation is in 3NF,but not in BCNF.
This relation has following FDs:
(Subject, Student) --- Teacher Teacher --- Subject (Teacher, Student) --- SubjectThis is a case of overlapping of candidate keys, because there are two composite candidate keys (Subject, Student) and (Teacher, Student) and Student is a common attribute in both the candidate keys. So, this database must be normalized according the BCNF.
This relation suffers again from the anomalies as discussed below:
For example, if we wish to delete the information that Kumar is study Physics, we cannot do so without losing the information that Prof. Neha teaches Physics.
These difficulties are caused by the fact that teacher is determinant but not a candidate key.
In order to make it in BCNF, teacher must be candidate key, so original relation is replaced by two projections ST (Student, Teacher) and TJ (Teacher, Subject).
All the anomalies which were present in SST, now removed in these two relations.
Practice Session:
Show that every two-attribute relation is in BCNF. That is, if r(X, Y) then r(X,Y) is in BCNF.
Solution: Let us consider the following cases:
a) X is the sole key of the relation. In this case, the nontrivial dependency X → Y has X as a super key since X c Y.
b) Y is the sole key of the relation. hi this case, the nontrivial dependency Y → X has Y as a super key since Y c Y.
c) Both X → Y and Y → X hold simultaneously. Then whatever PK we consider for the relation we will have either X or Y as its determinant. Either one of the two possible cases has already been considered under (a) or (b).
Consider the relation Supplier (Supplier-No, Part-No. Supplier-Name, Supplier-Control, Price) and assume that only the following FDs hold for this relation: Supplier-No —>Supplier-Name, Supplier-No ~ Supplier-Control. What type of data anomalies does this relation have in its present form? Transform it to 3NF if not already in that form.
Solution: This relation present insertion anomalies, deletion anomalies and update anomalies. In this relation we cannot enter a Supplier-Control until that supplier supplies a part (insertion anomaly). Notice that this is necessary to preserve the integrity constraint of the key. If a supplier stops temporarily supplying a particular part, then the deletion of the last tuple containing that Supplier-No also deletes the Supplier-Control of the supplier (deletion anomaly). Finally, if the Supplier-Control of a particular supplier needs to be updated, we must look for every tuple that contains that supplier as part of the key. If a supplier supplies many parts and we fail to update all the corresponding tuple, the database may end up in an inconsistent state. We can transform this relation into a 2NF as follows:
Supplier (Supplier-No, Supplier-Name, Supplier-Control) and Part (Part-No, Supplier-No, Price)Consider the relation for release RECORD (Title, Performer, Style, Price, Label, Producer) and the dependencies shown below. Indicate what the highest normal form of this relation is. Indicate a possible 3NF decomposition of this relation.
Title → Label, Style Style → Price Performer → ProducerSolution: The key of the relation is the composite attribute Title, Performer. As it stands the relation is in INF because there is at least one partial dependency on the key. For example, Performer – Producer. A possible decomposition may be Record (Title, Performer), Genre (Title, Label, Style), Producer (Performer, Producer- Name), Cost(Style, Price).

 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular