Multi-point Architectures

Applications that are conventionally used on terminal equipment put in implement a point-to-point communication, that is to say the part of the communication micro to go look for information to only one other point. Many other applications involve the cooperation of several processes. For example, a search in a distributed database in which information is spread across multiple sites, uses a simultaneous request for information to several centers. To make this request, the application and all associated protocol layers must manage multipoint. This way of communicating is more powerful than that which is to apply a first site, and once the response, a second, and so on.

The establishment of a multipoint communication is obviously more complex than that of a point-to-point simple communication. Before describing what standard setters retained in addendum 2 to ISO 7498-1, it is important to understand the two extremes possibilities a multipoint communication.

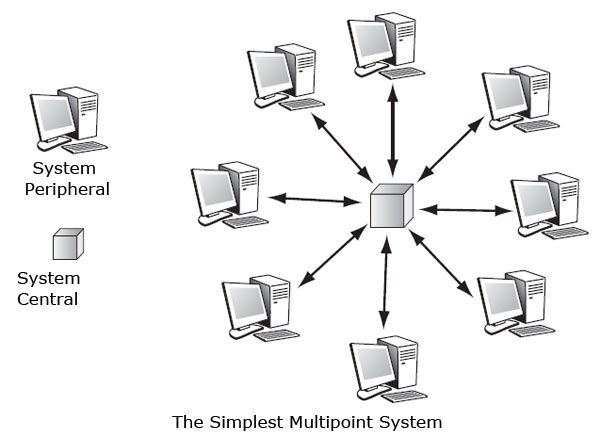
In the simplest case, there is a central system and peripheral systems. Only the central system can communicate with all peripheral sites, peripheral systems that can communicate with the central site. The advantage of this method is the simplicity of communications. The management of the assembly can be carried out by the center. This case is illustrated in FIG.

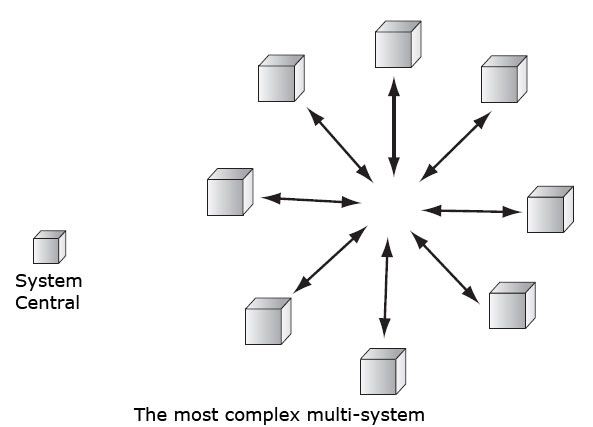
In contrast, most complex multipoint is one in which every system is a central system, that is to say that each site can communicate directly with any other site. We can see the overall complexity of this configuration, since the exchange management is fully distributed and that the coordination of systems is difficult to support. This case is illustrated in FIG.

Between these two extreme configurations, there is a hierarchy of possibilities. Standard setters have selected two, multipoint mobile communication center and multicenter communication.

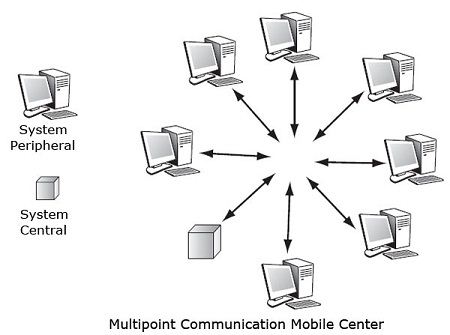
Multipoint mobile communication center is a slight improvement from the simplest multipoint: at a given moment, there is only one central system, but the primary site can vary in time. A complex multipoint system is always equivalent to a Multipoint Communication succession movable center.

This configuration is illustrated in FIG. The disadvantage may be its relative slowness when the multipoint system wants to parallelism.

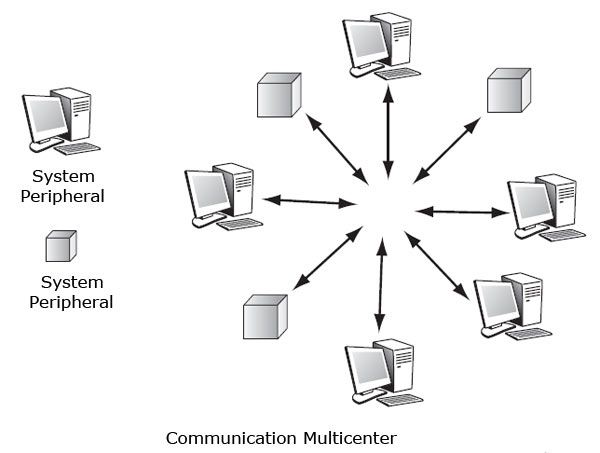
In the multicenter communication if N sites involved in the implementation of the multipoint communication, only up to Mr. sites can act as a central system, he is generally much less than N.

This configuration is illustrated in the figure, in which, on the sites of the network 8, 3 are mainframe and peripheral systems 5.

Using the two topologies defined by ISO, you can set up any multipoint environment. The simplest case is a special case multipoint centralized mobile communication center: just as the central site never changes. Similarly, the more complex case is nothing other than a multi-center system where N = M.

The second major concept of multipoint communication as defined in the basic standard for the notion of group needed to control communication. A multicast group is a set of entities that can be transmitter or receiver in a transmission multipoint data. This notion of the group is to define what happens during communication, specifically between that inside the group.

To simplify the definition of the behavior of groups, three classes are indicated:

• An unknown group in which each site does not know the exact constitution all the sites involved in the communication.

• A partially defined group, in which only a few specific sites known all of the group definition.

• A defined group, wherein all the sites know all of the definition of group.

Groups are sets perfectly defined which do not move in time. This concept, however, is too restrictive; a new system participating in an open set can be added in time. The groups must therefore be variable. To do this, we identified two groups of classes:

• Static groups in which the number of sites during a multipoint communication does not change. The number of sites is a fixed value, and the sites themselves can not change.

• Dynamic groups, in which systems can evade multipoint communication and other insert it. Obviously, in the case generally, group dynamics must be controlled and that a site can be added if did not receive prior approval. However, there are environments where all clients are welcome and are added to the group already listening. For example, if on a satellite channel, an advertising broadcaster transmits information, he has an interest in a maximum of receivers are tuned. In other cases, however, for safety and other reasons, it is necessary to prevent a non-endorsed website participating in a multipoint communication on strategic issues.

Multipoint groups can also be qualified. Was defined for these two types of groups:

• Conjured groups that define all the sites that are authorized to participate in a communication.

• The active groups that define the sites that actually participate in multipoint communication.