Cyclic Redundancy Check (CRC) An error detection mechanism in which a special number is appended to a block of data in order to detect any changes introduced during storage (or transmission). The CRe is recalculated on retrieval (or reception) and compared to the value originally transmitted, which can reveal certain types of error. For example, a single corrupted bit in the data results in a one-bit change in the calculated CRC, but multiple corrupt bits may cancel each other out.
A CRC is derived using a more complex algorithm than the simple CHECKSUM, involving MODULO ARITHMETIC (hence the ‘cyclic’ name) and treating each input word as a set of coefficients for a polynomial.
• CRC is more powerful than VRC and LRC in detecting errors.
• It is not based on binary addition like VRC and LRC. Rather it is based on binary division.
• At the sender side, the data unit to be transmitted IS divided by a predetermined divisor (binary number) in order to obtain the remainder. This remainder is called CRC.
• The CRC has one bit less than the divisor. It means that if CRC is of n bits, divisor is of n+ 1 bit.
• The sender appends this CRC to the end of data unit such that the resulting data unit becomes exactly divisible by predetermined divisor i.e. remainder becomes zero.
• At the destination, the incoming data unit i.e. data + CRC is divided by the same number (predetermined binary divisor).
• If the remainder after division is zero then there is no error in the data unit & receiver accepts it.
• If remainder after division is not zero, it indicates that the data unit has been damaged in transit and therefore it is rejected.
• This technique is more powerful than the parity check and checksum error detection.
• CRC is based on binary division. A sequence of redundant bits called CRC or CRC remainder is appended at the end of a data unit such as byte.
Requirements of CRC :
A CRC will be valid if and only if it satisfies the following requirements:
1. It should have exactly one less bit than divisor.
2. Appending the CRC to the end of the data unit should result in the bit sequence which is exactly divisible by the divisor.
• The various steps followed in the CRC method are
1. A string of n as is appended to the data unit. The length of predetermined divisor is n+ 1.
2. The newly formed data unit i.e. original data + string of n as are divided by the divisor using binary division and remainder is obtained. This remainder is called CRC.
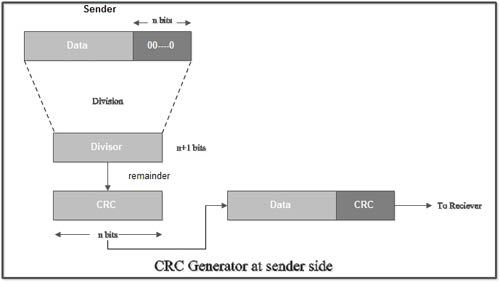
3. Now, string of n Os appended to data unit is replaced by the CRC remainder (which is also of n bit).
4. The data unit + CRC is then transmitted to receiver.
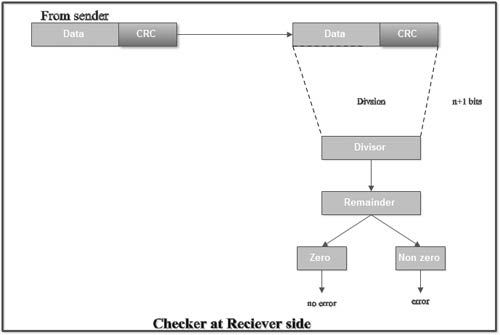
5. The receiver on receiving it divides data unit + CRC by the same divisor & checks the remainder.
6. If the remainder of division is zero, receiver assumes that there is no error in data and it accepts it.
7. If remainder is non-zero then there is an error in data and receiver rejects it.
• For example, if data to be transmitted is 1001 and predetermined divisor is 1011. The procedure given below is used:
1. String of 3 zeroes is appended to 1011 as divisor is of 4 bits. Now newly formed data is 1011000.
1. Data unit 1011000 is divided by 1011.
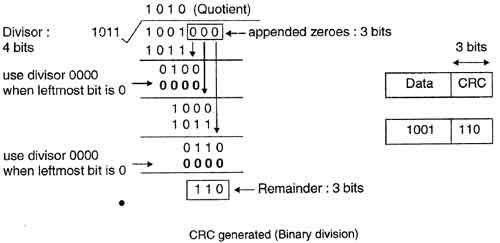
2. During this process of division, whenever the leftmost bit of dividend or remainder is 0, we use a string of Os of same length as divisor. Thus in this case divisor 1011 is replaced by 0000.
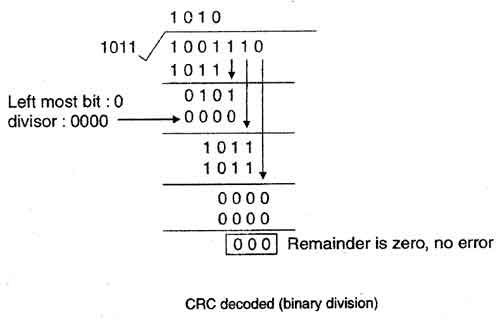
3. At the receiver side, data received is 1001110.
4. This data is again divided by a divisor 1011.
5. The remainder obtained is 000; it means there is no error.
• CRC can detect all the burst errors that affect an odd number of bits.
• The probability of error detection and the types of detectable errors depends on the choice of divisor.
• Thus two major requirement of CRC are:
(a) CRC should have exactly one bit less than divisor.
(b) Appending the CRC to the end of the data unit should result in the bit sequence which is exactly divisible by the divisor.
Polynomial codes
• A pattern of Os and 1s can be represented as a polynomial with coefficient of o and 1.
• Here, the power of each term shows the position of the bit and the coefficient shows the values of the bit.
• For example, if binary pattern is 100101, its corresponding polynomial representation is x5 + x2 + 1. Figure shows the polynomial where all the terms with zero coefficient are removed and x J is replaced by x and XO by 1.
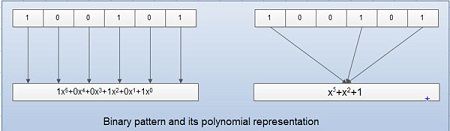 • The benefits of using polynomial codes is that it produces short codes. For example here a 6-bit pattern is replaced by 3 terms.
• The benefits of using polynomial codes is that it produces short codes. For example here a 6-bit pattern is replaced by 3 terms.
• In polynomial codes, the degree is 1 less than the number of bits in the binary pattern. The degree of polynomial is the highest power in polynomial. For example as shown in fig degree of polynomial x5 +x2 + 1 are 5. The bit pattern in this case is 6.
• Addition of two polynomials is based on modulo-2 method. In such as case, addition and subtraction is same.
• Addition or subtraction is .done by combining terms and deleting pairs of identical terms. For example adding x5 + x4 + x2 and x6 + x4 + x2 give x6 + x5. The terms x4 and x2 are deleted.
• If three polynomials are to be added and if we get a same term three times, a pair of them is detected and the third term is kept. For example, if there is x2 three times then we keep only one x2
• In case of multiplication of two polynomials, their powers are added. For example, multiplying x5 + x3 + x2 + x with x2+ x+ 1 yields:
(X5 + x3 + x2 + x) (x2 + x + 1)
= x7 + x6+ x5+ x5+ x4+ x3+ x4+ x3+ x2+ x3+ x2+ x
=X7+x6+x3+X
In this, first polynomial is multiplied by all terms of second. The result is then simplified and pairs of equal terms are deleted.
• Incase of division, the two polynomials are divided as per the rules of binary division, until the degree of dividend is less than that of divisor.
CRC generator using polynomials
• If we consider the data unit 1001 and divisor or polynomial generator 1011their polynomial representation is:
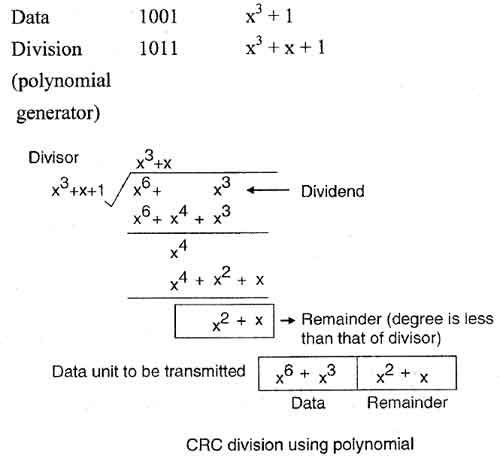
• Now string of n 0s (one less than that of divisor) is appended to data. Now data is 1001000 and its corresponding polynomial representation is x6 + x3.
• The division of x6+x3 by x3+x+ 1 is shown in fig.
• The polynomial generator should have following properties:
1. It should have at least two terms.
2. The coefficient of the term x0 should be 1.
3. It should not be divisible by x.
4. It should be divisible by x+ 1.
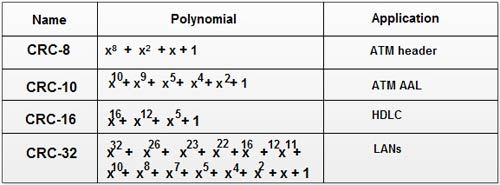
• There are several different standard polynomials used by popular protocols for CRC generation. These are:
 [/vc_column_text][/vc_column][/vc_row]
[/vc_column_text][/vc_column][/vc_row]
 Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular
Dinesh Thakur holds an B.C.A, MCDBA, MCSD certifications. Dinesh authors the hugely popular